I am a Ripon High School Geometry student. For my extra credit, I am trying to find a copy (or even an outline) of Euclid's proof of the pythagorean theorom. I found your site on the internet while searching through for "Euclid's Pythagorean Proof". So, I assume you have something on it.
Anything that you could send me, or any leads you could give me would be very helpful!
Thanks so much!
Sean
Sean:
Euclid actually gives two proofs of this theorem in his "Elements", one is in Book I and the other in Book VI. If you want a reference, there is a wonderful book containing the proof and some historical notes. It is
William Dunham, Journey Through Genius: The Great Theorems of Mathematicians, John Wiley and Sons, New York, 1990.
His notes on "Euclid's Pythagorean Proof" are on pages 48 to 50.
Here is an outline of the proof from Book 1 of Euclid's Elements.
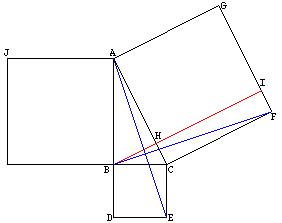
Construct the line through B which is parallel to CF and label the points where it intersects AC and GF by H and I respectively. Join B to F and A to E.
Using side-angle-side the triangles BCF and ECA are congruent. Since the angles ABC and CBD are right angles, ABD is a line and also parallel to CE. Thus triangles ECA and ECB have the same area and so the area of triangle ECA is half the area of the square on BC.
In a similar way, since the lines BI and CF are parallel, the area of triangle BCF is half the area of the rectangle HIFC. Thus the area of this rectangle is the area of the square on BC.
If you now construct the line from B to G and the line from C to J a similar argument shows that the rectangle AHIG has the same area as the square on AB.
Harley
To return to the previous page use your browser's back button.