by Jamie Hubbard
The Mayan number system was developed by the ancient Maya civilization of Central America. Similar to the number system we use today, the Mayan system operated with place values. To achieve this place value system they developed the idea of a zero placeholder. The Maya seem to be the first people who used a place value system and a symbol for zero. Beyond these similarities there are some significant differences between the Mayan number system and our modern system. The Mayan system is in base 20 (vigesimal) rather than base 10 (decimal). This system also uses a different digit representation. The Mayan numbers are based on three symbols:
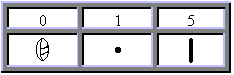
Some refer to these symbols as shells, pebbles, and sticks, which may have been the original counting items. These symbols can be combined to construct 19 digits (0 - 19). And with the use of the place value system any positive integer can be formed.
As mentioned previously this system works on the basis of place values in base 20. So the digits go from 0 - 19. 19 is represented by 4 pebbles and three sticks,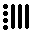 , which is the maximum number of symbols that can be in one place. If we add one pebble to 19, we will have 5 pebbles, which becomes 1 stick, giving us four sticks. These four sticks are represented in the second place as one pebble, and then the first place is left with a shell, zero,
, which is the maximum number of symbols that can be in one place. If we add one pebble to 19, we will have 5 pebbles, which becomes 1 stick, giving us four sticks. These four sticks are represented in the second place as one pebble, and then the first place is left with a shell, zero,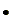
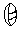 . Symbols in the second place are multiples of 20. Hence, five pebbles make one stick (5), and four sticks make one pebble and one shell (20).
. Symbols in the second place are multiples of 20. Hence, five pebbles make one stick (5), and four sticks make one pebble and one shell (20).
If we look at the base 10 system we will notice that the place values go up in powers of 10, for example: 100 = 102, 1000 = 103 (this applies to other bases as well). From this one would think that the place values in the Mayan system go up in powers of twenty. This assumption is not totally wrong but there is one twist. Instead of having a 202 column (400's column) the Mayan's used multiples of 360 (18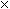 20), in the place of 400. The reason for this is that the main function of their number system was to keep track of time; their annual calendar consisted of 360 days. Following the 360's column, we have the 7200's column, which is 18
20), in the place of 400. The reason for this is that the main function of their number system was to keep track of time; their annual calendar consisted of 360 days. Following the 360's column, we have the 7200's column, which is 18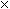 202 rather than 203. Note that the 18 takes the place of one 20.
202 rather than 203. Note that the 18 takes the place of one 20.
Now that we know the basics lets look at how we convert from the Mayan system to our decimal system. Consider the Mayan numeral:
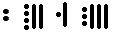
| In decimal form this would represent: | 2(18)(202) + 14(18)(20) + 6(20) + 18 = 2 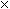 7200 + 14 7200 + 14 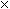 360 + 6 360 + 6 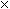 20 + 18 20 + 18= 14400 + 5040 + 120 + 18 = 19578 |
Addition of Mayan numerals, like in base 10, involves adding symbols, and carrying to the next place value when the previous one contains more than it can hold. We can simply add sticks to sticks and pebbles to pebbles.
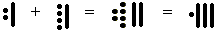
Here we can say:
- 2 pebbles + 4 pebbles = 6 pebbles and 1 stick + 1 stick = 2 sticks, so we have 6 pebbles and 2 sticks.
- 5 pebbles makes one stick, so 6 pebbles makes 1 stick and 1 pebble, so all together we get 1 pebble and three sticks, which makes 16.
When working with larger numbers we find that addition can get more complicated. Here is a problem that works through the possible complications:
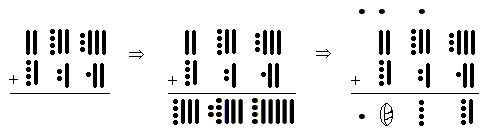
This is how it works:
- Start by simply adding the pebbles and sticks down each column.
- Now we must put this number into the Mayan base 20 format. In the one's column there are 5 sticks and 4 pebbles, 4 sticks combine to make 20 which is carried over as one pebble in the 20's column, leaving 1 stick and 4 pebbles.
- In the 20's column there are 6 pebbles plus the one that was carried over giving 7 pebbles and 3 sticks. When carrying from the second column to the third we carry when we get to 18 (three sticks and three pebbles). This is because the third column is 20
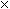 18 so it is build of multiples of 18. So we carry 18 to make one pebble in the 360's column and leaving 4 pebbles in the 20's column.
18 so it is build of multiples of 18. So we carry 18 to make one pebble in the 360's column and leaving 4 pebbles in the 20's column.
- Now in the 360's column we have 3 sticks and 5 pebbles (1 carried), 5 pebbles makes one stick, giving us 4 sticks which carry over to the 7200's column as a pebble. There is nothing left in the 360's column, which is represented by a shell.
If you feel confident you may be able to add and carry out the conversion between pebbles and stones at the same time, but be cautious about keeping everything in the right position. And you must always remember that from the 20's column you always carry 18 over to the 360's column. In other words, the 20's column cannot contain more than 17. But following the 20's column everything stays in base 20.
When subtracting we must also look at how many pebbles and sticks we have in each position. But in order to subtract we may need to make some sticks into pebbles. For example:
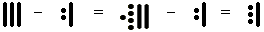
This is what we did:
- There are three sticks subtract 2 pebbles and 1 stick, so we must make one of the sticks in the group of three into 5 pebbles so we can subtract the two pebbles.
- Then we have 5 pebbles subtract 2 pebbles, and 2 sticks subtract 1 stick, leaving us with 3 pebbles and 1 stick.
Borrowing is also a necessary technique for subtracting Mayan numbers. Lets look at the following example:
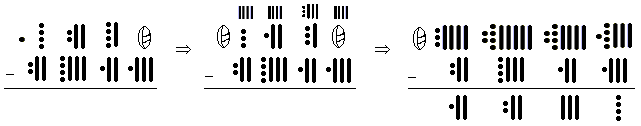
This may look really confusing but it is not that difficult. Here is what happened:
- Starting in the one's column we needed to borrow one pebble from the 20's column, giving us four sticks in the one's column, and leaving 3 pebbles and 1 stick in the 20's column.
- In the 20's column we must borrow from the 360's column, this column is made up of 18's so when we take one pebble we are taking an 18 rather than a 20 giving us 6 pebbles and four sticks.
- The 360's column is left with 1 pebble and 2 sticks, so we will borrow again from the adjacent column, to get 4 more sticks, giving 6 in total.
- Moving to the 7200's column, we borrow the one pebble in the adjacent column, leaving it with a shell, zero.
- Now it looks like we should be able to subtract, but we must take pebbles from pebbles, so we must change some sticks back into pebbles. We did this in the one's and 360's columns.
- Finally we can subtract. Working down the columns subtract pebbles from pebbles and sticks from sticks.
We can also easily convert from decimal to Mayan numerals. Lets look at 19578:
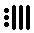
978 ÷ 18 = 54, remainder 6,
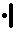
54 ÷ 20 = 2, remainder 14,
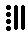
2 ÷ 20 = 0, remainder 2,
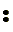
Working from the bottom up we get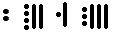 , which is what we started with when we converted from Mayan to decimal. The idea here is to start by dividing by 20, then divide by 18, and then continue dividing by 20 until we reach zero. We note the remainders as we divide and then write them out from the bottom to the top. In other words, the bottom remainder is worth the most value and the top remainder is worth the least value (1
, which is what we started with when we converted from Mayan to decimal. The idea here is to start by dividing by 20, then divide by 18, and then continue dividing by 20 until we reach zero. We note the remainders as we divide and then write them out from the bottom to the top. In other words, the bottom remainder is worth the most value and the top remainder is worth the least value (1 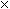 itself).
itself).
Here are some EXERCISES that you may want to try!
Studying Mayan Numerals makes a good connection between Math and Social Studies. Lessons on Mayan Numerals can be designed for a wide range of ages. For the primary grades it may be fun to look at this concept using shells, pebbles, and stones. This will help the students learn about place values, and the sorting and collection of different objects. For grades 4 - 6 manipulatives may also be used and then the students can go on to try some problems on their own (suggested exercises given). A Mayan Numerals lesson would also lend nicely to teaching about time and the cycle of a year.
Return to Math Central
To return to the previous page use your browser's back button.