|
Friezing at Washington State University
by Judith J. McDonald* and J. Harley Weston***Department of Mathematics, Washington State University, Pullman, Washington 99163-3113, USA.
**Department of Mathematics & Statistics, University of Regina, Regina, Saskatchewan, Canada, S4S 0A2.
1 Introduction
As mathematicians, we often talk about creativity, elegance and beauty in our work. We look for pattern, structure and form in the objects we're studying. These concepts are more commonly associated with the works of artists and artisans but they are also prevalent in mathematics. One place where the parallels between artistry and mathematics becomes evident is in the mathematical analysis of the structure and symmetry in artistic designs. In this article we will look at frieze designs from a mathematical perspective. Frieze designs are border decorations where a particular pattern is repeated indefinitely in a linear fashion. These designs show up in a variety of mediums in many cultures, from designs on clothing to the ornate architecture of places of worship and public buildings. We see a natural human tendency to use symmetry and repetition to visually enhance our surroundings.
In this article, we will start by determining the functions which map the plane onto itself, preserving the size and shape of any objects represented in it, and mapping a specified line back onto itself. These are the functions which preserves frieze patterns. We will then look at the algebraic structure of this collection of functions under the operation of composition, and show how the seven frieze groups are generated. We illustrate each frieze group algebraically and geometrically. We conclude our article with a tour of the Washington State University campus, looking at the ways in which frieze groups are exhibited and used in our immediate surroundings.
2 Isometries
An isometry of the plane is a function f which maps the plane onto
the plane and preserves distance. A consequence of this distance preserving
property is as follows. Consider any two points p and q in the plane.
Draw a circle centered at p and going through q. If we draw a circle around
f(p) of the same radius, then f(q) must lie on the boundary of this new circle.
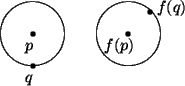
We are interested in all the isometries of the plane which have the additional
property that they map a given line ![]() back onto itself. For ease of
notation, we will assume that our line
back onto itself. For ease of
notation, we will assume that our line ![]() is the horizontal axis and
we describe it by
is the horizontal axis and
we describe it by
![]() where l1 varies over all real
numbers. An example of an isometry which maps
where l1 varies over all real
numbers. An example of an isometry which maps ![]() onto itself is
onto itself is
![]()
We classify the isometries f that map ![]() onto
itself by looking at the portion of the
plane that they leave fixed. There are three
cases to consider: f leaves no point fixed as in
the example above, f leaves exactly one point
fixed and f leaves more that one point fixed.
onto
itself by looking at the portion of the
plane that they leave fixed. There are three
cases to consider: f leaves no point fixed as in
the example above, f leaves exactly one point
fixed and f leaves more that one point fixed.
Suppose first that there is exactly one point, call it p = (p1, p2),
such that f(p) = p. Let l be the point on ![]() which is closest to p.
which is closest to p.

Since f(l) is on ![]() and the only point on
and the only point on ![]() which
is the appropriate distance from f(p) = p is l itself, it follows that f(l) = l. Since we assumed that p was the only point fixed by f, it must be the case that l = p and hence
p is on the line
which
is the appropriate distance from f(p) = p is l itself, it follows that f(l) = l. Since we assumed that p was the only point fixed by f, it must be the case that l = p and hence
p is on the line ![]() , and thus p = (p1, 0). Let q be any other point on
, and thus p = (p1, 0). Let q be any other point on
![]() . We know that f(q) is on the line
. We know that f(q) is on the line ![]() , Observe
that there are only two points on the line
, Observe
that there are only two points on the line ![]() which
intersect the circle centered at p = f(p) and going through q.
which
intersect the circle centered at p = f(p) and going through q.

Since f(q) ![]() q it follows that f(q) is the point on the opposite side
of p from q. Let r be any point which is not on
q it follows that f(q) is the point on the opposite side
of p from q. Let r be any point which is not on ![]() . Then by
ensuring that the distance from f(r) to p is the same as the distance from r to p, and that the distance from f(r) to f(q) is the same as the
distance and from r to q we see two possibilities for f(r).
. Then by
ensuring that the distance from f(r) to p is the same as the distance from r to p, and that the distance from f(r) to f(q) is the same as the
distance and from r to q we see two possibilities for f(r).
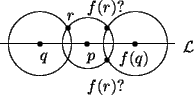
If we take s to be on a line perpendicular to ![]() through p, we see
that since f(s)
through p, we see
that since f(s) ![]() s it must be that f(s) is on the opposite side of the
line
s it must be that f(s) is on the opposite side of the
line ![]() from s. If we ensure that the distance from r to s is
the same as the distance from f(r) to f(s) we see that all the points r not on
from s. If we ensure that the distance from r to s is
the same as the distance from f(r) to f(s) we see that all the points r not on ![]() , get mapped to the opposite side of
, get mapped to the opposite side of ![]() .
Algebraically,
.
Algebraically,
f(r) = f(r1,r2) = (p1 + (p1 - r1 ), - r2 ) = (2p1 - r1, - r2) for all r = (r1, r2) in the plane. Thus this function is a 180 degree rotation R around the point p on the line ![]() .
.
Suppose next that there are at least two points p and q which are fixed by
f . Then f(p) = p and f(q) = q. Let r be any point on the line from p to q
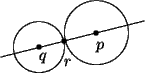
Since f(r) must be the same distance from f(p) = p as r is from p, and the same distance from f(q) = q as r is from q, we see that f(r) = r. Thus if f fixes more than one point, then it fixes every point along some line.
Consider first the case where f fixes exactly the line ![]() , viz.
f(l) = l for every l on
, viz.
f(l) = l for every l on ![]() and f(r)
and f(r) ![]() r for every r not on
r for every r not on
![]() . Let r be any point not on
. Let r be any point not on ![]() and let p and q be points
on
and let p and q be points
on ![]() . Since f(r) must be the same distance from f(p) = p as r is
from p and the same distance from f(q) = q as r is from q, and
f(r)
. Since f(r) must be the same distance from f(p) = p as r is
from p and the same distance from f(q) = q as r is from q, and
f(r) ![]() r we see that there is only one possibility for f(r).
r we see that there is only one possibility for f(r).
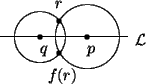
Algebraically we have that f(r) = f(r1, r2) = (r1, -r2) for
every point r in the plane. In this instance our function is a
reflection H through the horizontal line ![]() .
.
Now consider the case where f fixes exactly the line ![]() where
where
![]() .
Let p be any point on
.
Let p be any point on ![]() but not on .
Let l be the closest point on
but not on .
Let l be the closest point on ![]() to p. Again since f(l) must be on
to p. Again since f(l) must be on ![]() and it must be the same distance
from f(p) = p as l is, we see that f(l) = l.
and it must be the same distance
from f(p) = p as l is, we see that f(l) = l.
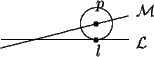
Thus both p and l are on ![]() and hence
and hence ![]() is perpendicular to
is perpendicular to ![]() , and intersects
, and intersects ![]() at l. Let r be any point which is not
on
at l. Let r be any point which is not
on ![]() . Since f(r) must be the same distance from f(p) = p as r is
from p, and the same distance from f(l) = l as r is from l, and in
addition f(r)
. Since f(r) must be the same distance from f(p) = p as r is
from p, and the same distance from f(l) = l as r is from l, and in
addition f(r) ![]() r we see that f(r) is uniquely determined.
r we see that f(r) is uniquely determined.
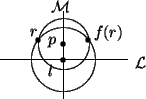
Algebraically, f(r) = f(r1, r2) = (l1+ (l1 - r1), r2) = (2l1 - r1, r2),
where l = (l1, l2) is the point where ![]() intersects
intersects ![]() .
This function is a reflection V through the vertical line
.
This function is a reflection V through the vertical line ![]() .
.
Suppose f fixes a line ![]() and a point r not on
and a point r not on
![]() . Let p be any point on
. Let p be any point on ![]() . Then, as above,
the line
. Then, as above,
the line ![]() through p and r is fixed by f. But then the line through any point on
through p and r is fixed by f. But then the line through any point on ![]() and any point on
and any point on ![]() is also fixed by f.
In fact, every point in the plane is fixed by f and hence
f is the identity mapping I.
is also fixed by f.
In fact, every point in the plane is fixed by f and hence
f is the identity mapping I.
Our final case to consider is the case where no
points are fixed by f .
That is, f(r) ![]() r for all points r in
the plane. Let p be a point
on the line
r for all points r in
the plane. Let p be a point
on the line ![]() . Then p is not fixed by
f. Since f(p) is also on
. Then p is not fixed by
f. Since f(p) is also on ![]() , it is some distance a units to the right or
left of p. We'll consider the
case where it is a units to the
right of p. The case where it is a units
to the left of p is similar.
Let q be the midpoint between p and
f(p). Then since f(q)
, it is some distance a units to the right or
left of p. We'll consider the
case where it is a units to the
right of p. The case where it is a units
to the left of p is similar.
Let q be the midpoint between p and
f(p). Then since f(q) ![]() q and the distance
between f(p) and f(q) is the same as the distance
between p and q, again we see that there is a unique
choice for f(q) - it must be a units to the right of q.
q and the distance
between f(p) and f(q) is the same as the distance
between p and q, again we see that there is a unique
choice for f(q) - it must be a units to the right of q.
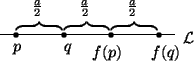
Let l be any other point on the line.
By maintaining the appropriate
distances between f(l) and f(p) and
f(l) and f(q), we see that f(l) must be a units to the right of l.
Let r be any point not on ![]() .
Again by maintaining the appropriate
distances between f(r) and f(p) and
f(r) and f(q), we see that
there are two possibilities for f(r):
.
Again by maintaining the appropriate
distances between f(r) and f(p) and
f(r) and f(q), we see that
there are two possibilities for f(r):
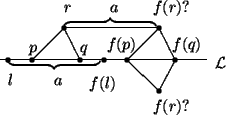
If f(r) is on the same side of ![]() as r, then for any other point s in the
plane, f(s) must be on the same side
of
as r, then for any other point s in the
plane, f(s) must be on the same side
of ![]() as s. Algebrically we
get that f(r) = f(r1, r2) = (r1 + a, r2)
for every point r in the plane.
We refer to this function as a translation T.
as s. Algebrically we
get that f(r) = f(r1, r2) = (r1 + a, r2)
for every point r in the plane.
We refer to this function as a translation T.
If f(r) is on the opposite side of ![]() from r then for any other point s in the
plane, f(s) must be on the opposite side
of
from r then for any other point s in the
plane, f(s) must be on the opposite side
of ![]() from s. Algebrically we
get that f(r) = f(r1, r2) = (r1 + a, - r2)
for every point r in the plane.
We call this function a glide-reflection and
denote it by G.
from s. Algebrically we
get that f(r) = f(r1, r2) = (r1 + a, - r2)
for every point r in the plane.
We call this function a glide-reflection and
denote it by G.
Thus our classification leaves us with
six types of functions:
- I - the identity where I(r1, r2) = (r1, r2).
- Ta - a translation where Ta(r1, r2) = (r1 + a, r2).
- Ga - a glide-reflection where Ta(r1, r2) = (r1 + a, - r2).
- H - a reflection through the horizontal line
 ,
where H(r1, r2) = (r1, - r2).
,
where H(r1, r2) = (r1, - r2).
- Vp - a reflection through a line perpendicular
to
 through the point (p, 0) where Vp(r1, r2) = (2p - r1, r2).
through the point (p, 0) where Vp(r1, r2) = (2p - r1, r2).
- Rm - a rotation of 180 degrees around the point (m, 0) where Rm(r1, r2) = (2m - r1, - r2).
3 Groups of Isometries
If we compose any two of these functions, then necessarily we
get back another isometry which maps ![]() onto
onto ![]()
Let's begin first by looking at what we get if we compose
two translations:
Thus a translation of a units composed with a translation of b units gives us a translation of a + b units. A set
Notice that Ta ![]() T0 = Ta = T0
T0 = Ta = T0 ![]() Ta.
An element E in
Ta.
An element E in ![]() is called an identity
of
is called an identity
of ![]() with the operation
with the operation ![]() provided that
for any U in
provided that
for any U in ![]() we have U
we have U ![]() E = U = E
E = U = E ![]() U.
The element T0 is the identity element of
the translations.
U.
The element T0 is the identity element of
the translations.
Notice next that Ta ![]() T-a = Ta - a = T0.
If U and V are elements in
T-a = Ta - a = T0.
If U and V are elements in ![]() such that U
such that U ![]() V = E = V
V = E = V ![]() U,
(where E is the identity of
U,
(where E is the identity of ![]() under
under ![]() ), we say that
V is an inverse of U. The element T-a is
the inverse of Ta.
), we say that
V is an inverse of U. The element T-a is
the inverse of Ta.
So far, we have only composed two functions
at a time. What happens if we compose three? Notice
that
and
Thus Ta
What happens if we compose
two translations in opposite order.
Notice Ta ![]() Tb = Ta + b = Tb + a = Tb
Tb = Ta + b = Tb + a = Tb ![]() Ta.
If for every U and V in
Ta.
If for every U and V in ![]() ,
we have U
,
we have U ![]() V = V
V = V ![]() U, then we say that the operation on
U, then we say that the operation on
![]() is commutative. Composition is a
commutative operation on the set of translations.
is commutative. Composition is a
commutative operation on the set of translations.
A set ![]() together with an operation
together with an operation ![]() is
called a group provided it is closed, contains
an identity, every element has an inverse, and
the operation is associative. If, in addition,
the operation is commutative, we say it is a commutative
group. We've seen that the translations form a commutative
group under composition.
is
called a group provided it is closed, contains
an identity, every element has an inverse, and
the operation is associative. If, in addition,
the operation is commutative, we say it is a commutative
group. We've seen that the translations form a commutative
group under composition.
Now let us look again at the full set of isometries
which map ![]() onto itself and examine the
various compositions of these functions. We can organize these compositions
into what is refereed to as a Cayley table. We begin by
constructing a six by six table
with a row and a column corresponding to each of the six types of
isometries which map
onto itself and examine the
various compositions of these functions. We can organize these compositions
into what is refereed to as a Cayley table. We begin by
constructing a six by six table
with a row and a column corresponding to each of the six types of
isometries which map ![]() to
to ![]() .
The j, k entry in the table represents the function we get
by taking the function corresponding to row j composed with the function
corresponding to column k. For example the entry in the second
(Tb) row and the third (Gc) column is Gb + c = Tb
.
The j, k entry in the table represents the function we get
by taking the function corresponding to row j composed with the function
corresponding to column k. For example the entry in the second
(Tb) row and the third (Gc) column is Gb + c = Tb ![]() Gc.
The completed Cayley table
is shown here:
Gc.
The completed Cayley table
is shown here:
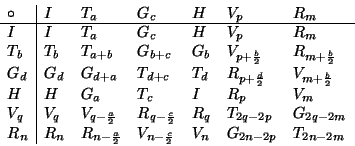
Notice that the composition of any two of these functions
is again an isometry which maps ![]() onto
onto ![]() and
hence this set is closed under composition.
The function I acts as
the identity. By choosing a,b,p,q,m,n correctly,
the reader can check that every element has an inverse
(recall that T0 = I).
We also leave it to the reader to check that composition
is associative. At this point, however, we would like
to point out that composition on this set is not commutative. For example,
Ta
and
hence this set is closed under composition.
The function I acts as
the identity. By choosing a,b,p,q,m,n correctly,
the reader can check that every element has an inverse
(recall that T0 = I).
We also leave it to the reader to check that composition
is associative. At this point, however, we would like
to point out that composition on this set is not commutative. For example,
Ta ![]() Vp = Vp + a/2 whereas Vp
Vp = Vp + a/2 whereas Vp ![]() T0 = Vp - a/2,
and hence they are not equal whenever a
T0 = Vp - a/2,
and hence they are not equal whenever a ![]() 0.
Thus the set of isometries which map
0.
Thus the set of isometries which map ![]() to
to ![]() form
a group under composition, but not a commutative group.
form
a group under composition, but not a commutative group.
A subset of a group which is also a group under the same operation
is called a subgroup. Given a collection
of elements U1,U2,...,Uk, from a group, we denote the
smallest subgroup which contains all of these elements by
<U1,U2,...,Uk>.
The set of translations is a subgroup of the group of
isometries which map ![]() onto
onto
![]() under the operation of composition.
under the operation of composition.
Let's begin with a translation of one unit to the right, T1
What is the smallest subgroup, ![]() , which contains this element?
It must have an identity, so T0 = I must be in
, which contains this element?
It must have an identity, so T0 = I must be in ![]() .
The inverse of T1 namely T-1 must also be in the
set. It inherits associativity from the big group, so
the last thing we need to ensure is that it is closed
under composition.
Since T1
.
The inverse of T1 namely T-1 must also be in the
set. It inherits associativity from the big group, so
the last thing we need to ensure is that it is closed
under composition.
Since T1 ![]() T1 = T2 the function T2 is in
T1 = T2 the function T2 is in ![]() .
Similarly T1
.
Similarly T1 ![]() T2 = T2 is also in
T2 = T2 is also in ![]() , as is
T-1
, as is
T-1 ![]() T-1 = T-2. In fact
T-1 = T-2. In fact
is the smallest subgroup which contains T1.
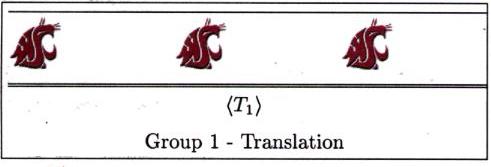
Starting with a blank page (plane) except for one cougar head,

applying each translation from ![]() to the plane and shading in the image of the cougar head,
we get the pattern:
to the plane and shading in the image of the cougar head,
we get the pattern:

Going back to our collection of isometries which
map ![]() to
to ![]() , we want to examine the
subgroups we can generate taking subsets of
the set
, we want to examine the
subgroups we can generate taking subsets of
the set
{T1, G1, H, V0, R0}.
Since the identity I is contained in
every subgroup, we do not need to include
it as one of the subgroup generators.
We get a collection of finite subgroups as follows:
The remaining subgroups generated by possible combinations of the functions from our set generate infinite subgroups. These seven infinite subgroups are the frieze groups.
4 The Frieze Groups
In this section we present the frieze groups both algebraically
and geometrically. Each picture represents the pattern you
would get (repeated indefinitely to the left and right of course),
if you apply every transformation in the subgroup generated
by the functions listed, to a single cougar head sitting
in the plane.
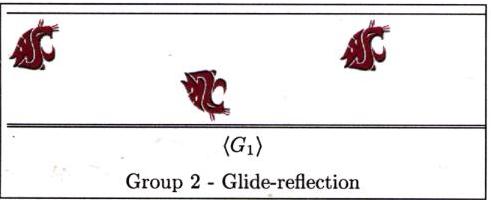

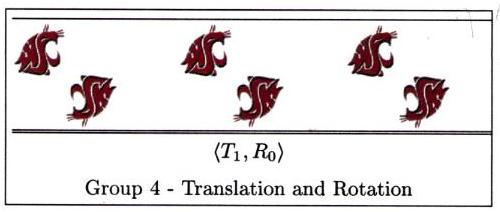

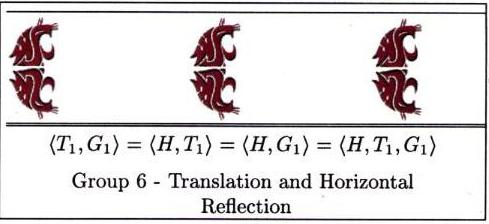
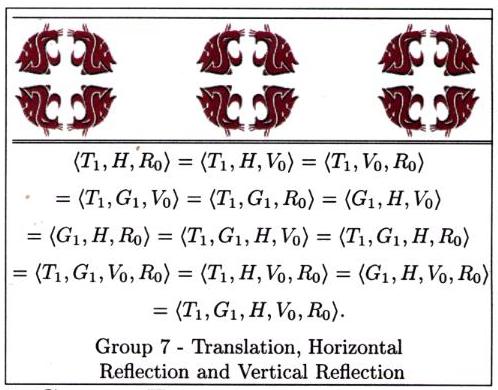
Now it's time to head out for a tour of the campus. We'll look for frieze designs on and in buildings, at the bookie, and even in the parking lots. See if you can classify each of the frieze designs below, and then head out for your own search.
We can see frieze groups on traditional decorations on buildings,

![]()

and their railings:


In fact, the basic construction method used on campus forms a nice pattern:


We found some designs showed up out of practicality,


and others had something to do with their functionality.
Wow - the friezing on these tire treads is all from
the same group. Notice that they don't have a
horizontal or vertical reflection. Interesting!



We found some friezing with a bit of a twist


and the clock tower has quite a bit:

We see friezing on art work and jewelry:



Even nature can't resist friezing,

although occasionally even humans can:

Well, we'd best head back to the office, and look here's one last example of a frieze group.

Bibliography
- B Jinny Beyer, Designing Tessellations,
Contemporary Books, Chicago, Illinois, 1999.
G Joseph A. Gallian, Contemporary Abstract Algebra, D. C. Heath and Company, Lexington, Massachusetts, 1994.
WC D. K. Washburn and D. W. Crowe, Symmetries of Culture: Theory and Practice of Plane Pattern Analysis, University of Washington Press, Seattle, Washington, 1988.
