Arc Midpoint Computation
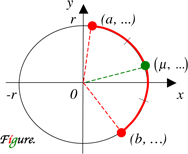
If an origin-centered arc of radius $r$ (see Figure) has the ends at $x = a, x = b$ and midpoint at $x = \mu,$ then
\[2 \mu = \pm \sqrt{(r + a)(r + b)} \pm \sqrt{(r - a)(r - b)}\; , \]
where the first radical gets “−” iff the arc has a negative x-intercept, and the second radical gets “+” iff the arc has a positive x-intercept.
The same relationship holds for y-values.
Proof
Denote $p=a/r, q=b/r, s_t=(1+t)/2$. Consider angles, $\alpha=\cos^{-1}p, \beta=\cos^{-1}q$, and $\gamma=cos^{-1}(\mu/r)$. There are four cases.
Case 1. The arc does not have $x$-intercepts. Then $\gamma=(\alpha + \beta)/2, \mu=r\cos{1 \over 2}(\cos^{-1}p + \cos^{-1}q)$. Identity $\cos^{-1}p + \cos^{-1}q = 2\cos^{-1}(\sqrt{{s_p}{s_q}} - \sqrt{{s_{-p}}{s_{-q}}})$ gives $\mu = r(\sqrt{{s_p}{s_q}} - \sqrt{{s_{-p}}{s_{-q}}})$. Hence, $2\mu = \sqrt{(r+a)(r+b)} - \sqrt{(r-a)(r-b)}$; |
 |
Case 2.The arc has positive $x$-intercept, but does not have negative one. Then $\gamma=|\alpha - \beta|/2, \mu=r\cos{1 \over 2}(\cos^{-1}p - \cos^{-1}q)$. Since $|\cos^{-1}p - \cos^{-1}q| = 2\cos^{-1}(\sqrt{{s_p}{s_q}} + \sqrt{{s_{-p}}{s_{-q}}})$, we get $\mu = r(\sqrt{{s_p}{s_q}} + \sqrt{{s_{-p}}{s_{-q}}})$. Hence, $2\mu = \sqrt{(r+a)(r+b)} + \sqrt{(r-a)(r-b)}$;
Case 3. The arc has negative $x$-intercept, but does not have positive one. This part of proof is similar to case 2 with $\gamma = \pi - {1 \over 2}|\alpha - \beta|$;
Case 4. The arc has two $x$-intersepts. This part of the proof is similar to case 1 with $\gamma = \pi - {1 \over 2}(\alpha + \beta)$
Proof for y-values can be received using the same approach or otherwise. Q.E.D.
Arc midpoint computation was suggested by first attempt shown in [1]. Details of proof involved identities received from [2].
References
- Oleksandr (Alex) G. Akulov (2009). Dot product finds arc midpoint. Math News, U of W. Volume 111, Issue 6, p. 5.
- Gregory V. Akulov (2010). The slope of the angle bisector relationship in applied and theoretical problems. Vinculum, SMTS. Volume 2, Number 1, p. 49.
Copyright © February, 2011 by Oleksandr (Alex) G. Akulov
|

