Networks as a Problem Solving Technique
Denis Hanson, Department of Mathematics & Statistics,
University of Regina
Diane Hanson, Saskatchewan Education (O.M.L.O.),
Regina, Saskatchewan
1. Introduction.
The National Council of Teachers of Mathematics has stated: " ... that all students need to learn more, and often different, mathematics and that instruction in mathematics must be significantly revised." ([1], page 1). In order for people to meet the needs of life in a rapidly changing world, curriculum goals in mathematics must prepare students to develop the skills and knowledge of concepts necessary to meet the needs of the average consumer; to develop the ability to analyze and interpret quantitative information; to develop logical thinking skills, and an appreciation of mathematics; to develop the desire, confidence, and ability to solve problems; to communicate mathematically; and to pursue further study in mathematics and mathematically related areas (see[3], page iii). It is through these goals that students will become mathematically literate. In order to attain these goals, "problem solving should be the central focus of the mathematics curriculum. (It) should permeate the entire program and provide the context in which concepts and skills can be learned." ([1], page 23). These sentiments are repeated in Mathematics, Charting the Course, Summary and Recommendations, [4].
"Toward this end, we see classrooms as places where interesting problems are regularly explored using important mathematical ideas. Our premise is that what a student learns depends to a great degree on how he or she has learned it... ." ([1], page 5). Students should be given the opportunity to model and solve problems from every day activities, and, through this active process, develop an appreciation of the process of solving problems. "Mathematics becomes useful to a student only when it has developed through a personal intellectual engagement that creates new understanding." [2]
In this note we look at a problem from Discrete Mathematics. Although the N.C.T.M. 'Standards' recommends the study of Discrete Mathematics (counting, permutations, combinations, graph theory, etc.) be integrated throughout the later years (grades 9 - 12), there are numerous examples that lend themselves to the middle years (and earlier!). The problem that we consider involves mathematical modeling of a familiar situation and has the feature that the solutions are not unique. Finding the solutions (actually developing an appropriate algorithm) requires an understanding of the model from the real-life situation, and, the different approaches developed by the students provide ideal opportunities for classroom discussion. The problem and the concepts involved are easily adapted to other real-life situations. We conclude with some other problems that may be modeled in a similar manner.
2. The problem.
There has been a huge blizzard and all the streets are blocked. Suppose that you and your friends have a map of the roads between houses and further that you know the time, in minutes, that it takes a snowplow to clear different sections of road. Your problem is to devise a scheme for the snowplow operator to follow in order for him to clear (just) enough roads such that each of you can get to any other friend's house, and further, find such schemes that accomplish this in a minimum amount of snowplowing time. We allow paths between two friends' houses to pass by other friends' houses along the way, that is, they are not always direct paths.
3. The mathematics.
It is not important in this article that we be too formal in our definitions and proofs and we deal with most things on an intuitive level. When we talk about a graph or a network in Discrete Mathematics, we mean a set of points (vertices) and edges (lines) that join some pairs of these points. Sometimes we attach a value to an edge which we call its weight. A network is connected if you can get from any one point in the network to any other point by 'walking' along the edges. Figure 1 is an example of a connected graph with 9 points and 16 edges. (It is not always the case that edges don't cross one another as in this example but for our purposes we will restrict ourselves to such 'planar' graphs).
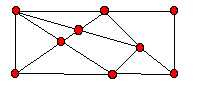
A Graph or Network
Figure 1
A circuit in a graph is a sequence of edges that allows us to travel from a point through other points and return to the initial point. We may pass through the same point of the graph more than once. If the points on the circuit are distinct we call it a cycle. For example, in figure1, travelling around the 'outside' of the graph determines a cycle of length six. Another special type of graph is a tree - a connected graph without any cycles (see figure 2). You might observe that a tree with n points has exactly n-1 edges (just enough edges to connect all the points). For example the tree in figure 2 has 9 points and 8 edges.
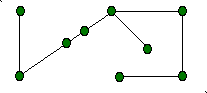
A Tree
Figure 2
4. The model and solution.
We model our problem with a weighted graph as shown in figure 3 where the points of the graph are the houses, the edges correspond to roads and the weights on the edges give the number of minutes that it takes to plow that road.
To solve the problem the student needs to make several observations. Remember that we must connect all of the houses. To do so in the most efficient manner we must build a tree connecting all the houses so that the total weight of the edges on the tree that we select is as small as possible. The total weight of the tree corresponds to the total time needed by the plow.
The reason we want a tree is that if we include a cycle in the set of roads that we select, we could discard one of the roads on the cycle and still have all of our houses connected (with less plowing required). The algorithm that solves the problem (known as Kruskal's Algorithm, see [5], page 54) is an example of what is called a "greedy algorithm" - we select roads in the greediest possible way. It is clear that we want to pick as many roads with smallest weights (times) as possible. If we choose all of them (the roads of weight 10 in our example) we would be including cycles, so we choose as many as possible without creating a cycle. Note that there is more than one way to do this. Having chosen as many as possible of weight 10, we now look at the roads with second smallest weights (the roads of weight 20 in our example)
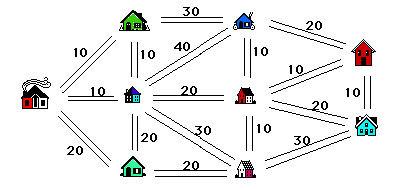
Figure 3
and add as many of these as possible to our list, all the while being careful to avoid creating a cycle. Continue in this vein until we have selected one less road than the number of houses (8 roads in our example). The result is a tree with minimum total weight (time). Two solutions are illustrated in figure 4. Note however, that although the solutions are distinct, the total weight of the selected edges, i.e., the total time required is 10 +10 + 10 + 10 + 10 + 10 + 20 + 20 = 100 minutes in both cases. This is always the case.
How many different solutions can you find?
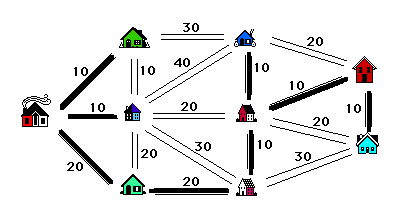
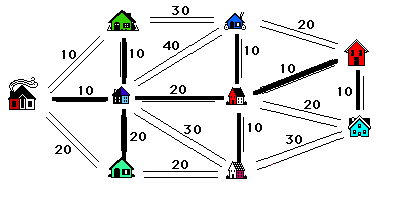
Figure 4
5. Further directions and problems.
The concepts of graph theory lend themselves to many applications. A network ideally models communication networks, airline routes, electrical networks etc. where the weights assigned to the edges could be long distance rates, distances, resistances, whatever... . Graphs can easily model the societal relationships between students - this time an edge represents a friendship between two people. Sometimes we use directed edges (arrows) in our models, for one way streets for example. Beyond these applications of course is the study of graphs for their own sake. There are many introductory combinatorics books containing sections on graph theory and a number of 'elementary' texts on the subject (see [5] for example). Unfortunately these are usually at least at the secondary level and need to be adapted down for the K - 8 classrooms. As long as the size of the examples studied is not too large, many of the ideas are not beyond the elementary and middle year student.
We close with some suggestions for further study.
i) Suppose in the snowplow problem of section 2, the plow operator knows he has to plow out roads forming a tree but since he is paid by the hour, he plows a tree of maximum rather than minimum time (cost). How does he pick the roads now?
ii) Suppose instead of the snowplow problem of section 2 we take the map of figure 3 to represent distances between houses. How can we find the shortest distance from our house (pick your own) to each of our friend's houses? The solution will be different for each person's house. This problem is significantly more difficult but, as long as we keep the size of our problem small, it is reasonable and should stimulate some good classroom discussion.
iii) Suppose that you have a map of part of the city which constitutes a snowplow's area to be cleaned (see figure 5). Is there a plan that allows the snowplow to go down each street exactly once and end up at its starting point? If not, can we minimize the number of streets that it must travel (not necessarily plow) more than once? This problem is slightly more difficult than the main question in this paper but easier than question ii). It turns out to be quite easy in the case where an even number of roads (edges) leave each house (point) as in figure 5. The solutions in this latter case are called Euler circuits. If there are exactly two houses without an even number of roads leaving them then there is a solution where the plow starts at one of these houses and finishes at the other.
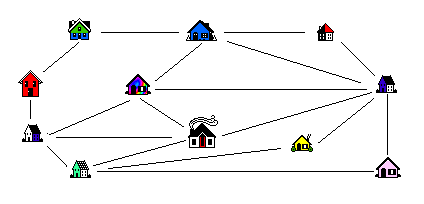
Figure 5
The problems mentioned in this article are discussed in a grade 5 model unit contained in Mathematics: A Curriculum Guide for the Elementary Level, [3]. Clearly the size and complexity of the problem can be adapted to suit almost all grade levels. For example, problems can be changed using a papergirl's route as she delivers delivers papers on both sides of the street, or a garbage truck route (whether the garbage is collected from both sides of the street at the same time alters the problem). These problems offer ideal opportunities for students to test and discuss trheir ideas in group situations. Students may be assessed through the use anecdotal records, written assignments or observation checklists.
References
1. Curriculum and Evaluation Standards for School Mathematics, N.C.T.M., 1989.
2. Everybody Counts, A Report to the Nation on the Future of Mathematics Education, National Research Council, Washington D.C., 1989.
3. Mathematics: A Curriculum Guide for the Elementary Level, Saskatchewan Education, 1992.
4. Mathematics, Charting the Course, Summary and Recommendations, Saskatchewan Education, (1989).
5. Robin J. Wilson, Introduction to Graph Theory, 3rd. edition, Longman Group Ltd., 1985.
To return to the previous page use your browser's back button.