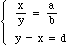
given constants a, b and d with b not 0. From the first equation we have,
In a recent article, On My Mind - Conceptual Understanding and Computational Skills in School Mathematics, Scavo and Conroy consider the following problem:
Two numbers are in the ratio of 2 to 5. One number is 21 more than the other. What are the two numbers?
The authors look at one student's solution:
5 - 2 = 3; 21/3 = 7; 2*7 = 14 and 5* 7 = 35
and wonder as to whether or not to give full marks to the student.
Scavo and Conroy present the following algebraic verification of the student's method:
"We want to solve the equations
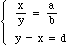
given constants a, b and d with b not 0. From the first
equation we have,
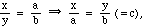
for some unknown constant c.
The constant c corresponds to the `magic' number
7 in the solution. From the right-hand side we see that
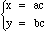
for some unknown constant c. The equations yield
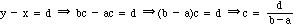
provided that b - a is not 0. Substituting we obtain
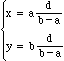
which solves ..." our problem.
I would like to offer an alternate, visual, demonstration of the student's method that I believe demonstrates conceptual understanding and computational skills in a way that the idea will remain with the problem solver, as opposed to the algebraic method given which I believe often does not.
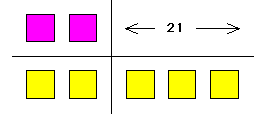
|
Two numbers are in the ratio of 2 to 5 (think of two parts and five parts), and one number is 21 more than the other |
and thus
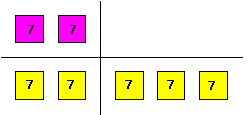
|
i.e. the parts have size 7 and the numbers are 14 and 35. |
So, quite simply, one number has two parts; another has five parts; their difference of three parts has size 21; each part has size 7 and ... .
Of course, in general if two numbers are in the ratio of a to b and one is d more than the other:
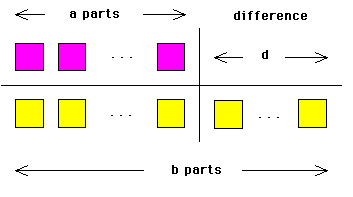
and each of the (b - a) parts has size d/(b - a) so that the numbers are ad/(b - a) and bd/(b - a). My experience tells me that students (particularly in middle years) readily understand the logic of this approach and furthermore such problem solving skills remain with them.
Reference
Scavo, T. R. and Conroy, N. K., On My Mind - Conceptual Understanding and Computational Skills in School Mathematics, Mathematics, Teaching in the Middle School, NCTM Vol. 1, No. 9, 1996, 684-686.
To return to the previous page use your browser's back button.