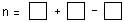
Being a middle years mathematics pilot teacher has allowed me opportunities to experiment with the new mathematics curriculum and several new teaching strategies. Prior to this year, when the topic of problem solving came to mind my focus would have been the Algebraic Problem Solving Method. The following is a description of how my focus changed.
Students were taught nine problem solving strategies, which were found in the new curriculum guide, and given examples of each. The nine strategies included guess and check; using a simple/related problem; making a systematic list, chart, table, or diagram; working backwards; using a number sentence/equation; examining and eliminating possibilities; using deductive reasoning; breaking a problem into sub-problems; and recognizing patterns. So far not much change had occurred in my teaching.
Then students were presented with a problem they had never seen before. Using any of the nine strategies the students were asked to record their attempts at solving the problem in a math journal. The journal entry was to include what the students were thinking while they were doing the problem as well as any calculations which were necessary. After two to three minutes of writing time the solution to the problem, different strategies which could have been used, and various student answers were discussed. The first attempts did not produce much writing as students were not familiar with the process. The students wanted examples of how to do similar problems and were reluctant to think on their own. Undaunted the class plodded forward and the results were well worth it. After recording 25 problems in their math journals there was more than one way to solve a problem. They also discovered that they could solve a problem they had never seen before on their own. The students had also discovered independent learning.
Using the nine strategies to solve problems changed my focus regarding problem solving. Similarly the students were changed, although they still are reluctant to try unfamiliar problems. It is my belief that regular exposure to these type of problems is necessary to solidify the strategies in the minds of the students. I hope this case study has been interesting. I am sure many of you have tried something similar; if not maybe you will in the future. Enjoy the struggle.
One sample problem which I gave to my students is taken from the Canadian Mathematics Competition, Pascal Contest, grade 9, Wednesday, February 24, 1993.
| Three cards number 1, 2, and 3 are placed one to a box in the equation shown. The number of different answers that can be obtained for n is |
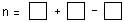
|
(A) 9 (B) 6 (C) 3 (D) 2 (E) 5
Here are some of the answers I received.
Shyla Rice
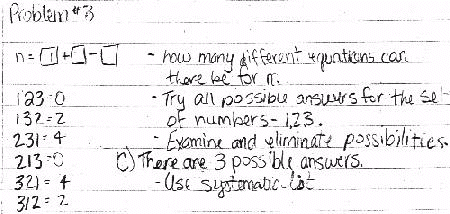
Alison
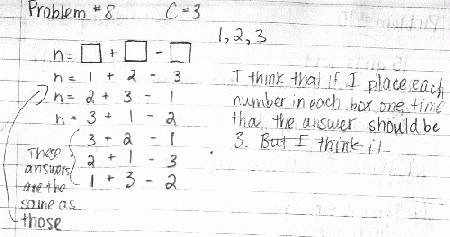
Jennifer Bohn
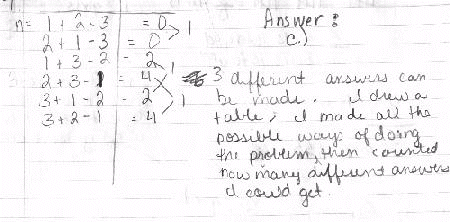
Jennifer Stiglitz

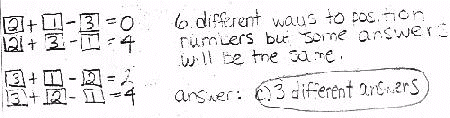
To return to the previous page use your browser's back button.