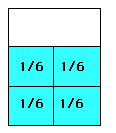
1/6 + 1/6 + 1/6 + 1/6 = 2/3
4/6 = 2/3
Introduction:
A full understanding of rational numbers for any middle year's student involves an understanding of rational numbers in all of its interpretations. These interpretations can be named in different ways, but in summary form they can be grouped under the headings or concepts of quotient, measure, ratio, decimal, and operator. If we take any rational number (fraction) objective from the new middle years' curriculum, for example grade 7, N-59 (use manipulatives, pictures, and symbols to compare and/or order fractions) we can address specifically the measure interpretation, in particular, the concepts of part/whole, area of a region covered, and equivalence.
Materials:
The new middle years' curriculum guide stresses the use of concrete materials as an aid to middle years' children understanding fractions. The curriculum guide recommends that for fraction activities at this level, the following materials be available:
* number lines
* metric rulers
* pattern blocks
* pie shapes
* paper strips for fractions
* fractional circles or squares
* geoboards
For this particular lesson (to address objective N-59 at the grade 7 level), the curriculum suggests that fractional strips or circles be used and that students should place these strips in order of increasing size.
Introductory Activity:
A useful beginning activity would be for each child to construct a personal fractional strip kit. This kit can be used for this specific lesson, and also for many other fraction activities. Making Mathematics (Gage, 1994) illustrates the use of paper strips for many of their suggested grade 7 fraction activities. The teacher guide for Making Mathematics 7 has blackline masters for paper strips. Kieren (1992) has used a fraction kit with grade 7 and 8 students in learning fractions. His kit consists of:
1. one whole sheet of paper--81/2 x 11--white
2. two half sheets (each half of an 8 1/2 x 11 sheet)--orange
3. three one-third sheets--yellow
4. four one-fourth sheets--pale pink
5. six one-sixth sheets--blue
6. eight one-eighth sheets--green
7. sixteen one-sixteenth sheets--bright pink
8. twelve one-twelfth sheets--beige
9. twenty-four one-twenty-fourth sheets--purple
It would be recommended that each student have a personal kit.
Each of the above colored sheets of paper can be thought of as a rectangular `pizza' cut into a specific numbers of parts. Children can be asked to say what one piece of each `pizza' would be called, what 5 pieces would be called, etc. They can then be asked to determine if 5 pieces of any of their `pizzas' is more than one, and, if so, which `pizzas.' They could then be asked to reassemble their `pizzas' into the separate colors and state how many parts of each comprise one-whole, one-half, etc. These are review activities, but are necessary to do before ordering fractions can be addressed.
Main Activity:
Children can take from their kits specific pieces (e. g. 3/8) and be asked to find other kit pieces which show the same amount (e. g. 6/16; 9/24). They can do this by laying their kit pieces on top of or under each other. They are comparing these fractional amounts, but they are also exploring equivalence. You can repeat this same activity for any fraction which has an equivalent.
A continuing activity would be to have the children select one fraction (e. g. 3/4), place it on their desk, and put under it other fractions which add to give 3/4. For example, one child may place 1/2 and 1/4 under the 3/4; another may place 1/8, 1/8, 1/8, 1/8, 1/16, 1/16, 1/24, 1/24, and 1/24 under the 3/4. Both children would be "correct." These fraction strips may or may not be ordered from the largest amount (1/8) to the smallest amount (1/24). If they are not ordered, the children can then be directed to order them. This activity can be repeated with any beginning fractional amount.
It is evident from the previous activity that many different viable "correct" answers will be demonstrated. Why not post these answers! For example, all the children could be determining a combination of kit pieces that would show the same amount as one whole, two-thirds of one, five-fourths. etc. A recent study in Edmonton, conducted by Kieren (1992), illustrated the following different coverings that nine grade 7 children made for two-thirds.
1.

1/6 + 1/6 + 1/6 + 1/6 = 2/3
4/6 = 2/3
2.
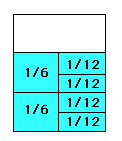
2/6 + 4/12 = 2/3
3.
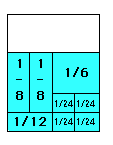
2/8 + 1/6 + 1/12 + 4/24 = 2/3
2/8 + 2/6 + 1/12 = 2/3
4.
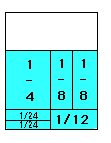
1/4 + 1/8 + 1/8 + 1/12 + 1/24 + 1/24 = 2/3
1/4 + 2/8 + 3/24 = 2/3
5.
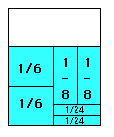
1/6 + 1/6 + 1/8 + 1/8 + 1/24 + 1/24 = 2/3
2/6 + 2/8 + 2/24 = 2/3
2/6 + 1/4 + 1/12 = 2/3
6.
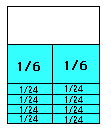
1/6 + 1/6 + 1/24 + 1/24 + 1/24 + 1/24 + 1/24 + 1/24 + 1/24 1/24 = 2/3
7.
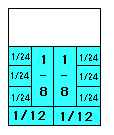
1/8 + 1/8 + 1/12 + 1/12 + 1/24 + 1/24 + 1/24 + 1/24 + 1/24 + 1/24 = 2/3
2/8 + 2/12 + 6/24 = 2/3
1/4 + 1/6 + 1/4 = 2/3
2/4 + 1/6 = 2/3
1/2 + 1/6 = 2/3
8.
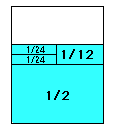
1/2 + 1/12 + 1/24 + 1/24 = 2/3
9.
1/3 + 1/3
1/6 + 1/6 + 1/6 + 1/6
1/12 +1/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12
1/24 + 1/24 . . .
Interpretation:
The above nine coverings can be grouped as follows:
A. Recording as unit fractions [6 & 8 (& 9)]
B. Recording as combined unit fractions (1, 2, & 4)
C. Recording as combined and re-configured unit fractions (3, 5, & 7)
D. Aesthetic coverings (all could be accepted as such, but # 7 is especially nice)
These coverings of 2/3 can all be accepted as "correct" as they all demonstrate viable answers. It is evident to a teacher that each of the nine children above understood their task and could demonstrate appropriate mathematical activity in carrying out their task. But the different arrangements and recordings have much to say about the sophistication or maturity of fraction thought on the part of the children. # 6 and 8 recorded exactly what constituted their arrangement and made no attempt to add the fractional amounts ( e. g. 8/24) that were the same or to reconfigure to another amount (e. g. 8/24 to 1/3). # 1, 2, and 4 did combine the fractional amounts that were the same (e. g. 1/6 + 1/6 became 2/6), but made no attempt to reconfigure the parts (e. g. 2/6 to 1/3). Then there were some children who both combined and reconfigured ( e. g. 3, 5, and 7), with # 7 combining and reconfiguring twice. # 9 was trying to find all the unit possibilities for each type of fraction and was not interested in combining or reconfiguring. His intent was to build a chart which showed all these same unit possibilities.
In the above activity, the children are getting much experience in comparing fractional amounts, exploring equivalence, and ordering fractions. An activity like the above can be conducted with one-whole as the amount to be covered, five-fourths, and so on. What is important to remember, in this open-ended or proscriptive activity, is that many "correct" answers will be possible. Children will respond to this activity by demonstrating their fraction knowledge in their activity of covering. The activity thus becomes a fraction-action-space for their knowledge to be demonstrated and an observational and assessment space for our knowledge of how children make sense of fractions to be demonstrated. As children are making sense of the math, we are making sense of their sense-making. Instruction or learning thought of in this manner is also assessment.
In doing the above activity and posting their work, the children will have the opportunity to see what coverings others have made; they get the chance to question other coverings, if they don't agree or don't understand; they get the chance to argue and convince others of their coverings; to justify the work they have done to others (including the teacher), and generally to "behave like mathematicians." They will learn from each other and children like # 6 will most likely learn from a peer how to combine or reconfigure. In all of this activity, the teacher can be asking appropriate questions, encouraging postings and recordings of work to be made and justified, perhaps making a personal posting to share with the children (not necessarily a # 7). The teacher and the children, working together in the above manner, constitute what I call a mathematical conversation, where the communication and the purpose of the activity all focus on the topic (of covering 2/3), and where the actual activity of the children is dominant. The activity reported above in a 1992 (Kieren) research study, and a similar one in a grade 3 (Maeers, 1993) study, have both demonstrated this same variety in solutions to the problem, and the same intense activity by the children in creating their solutions. These children all felt a satisfaction in knowing, a confidence in communicating, a sense of trust in acceptance of their work by others, a willingness to engage in argument and justification of their work, and a sense of mathematical power because they knew they were "right."
I challenge any middle years teacher to try the above activity, or variation of it, and write in your comments about the children's reactions to the activity. I would also question how much "teaching" in the traditional "direct-transmissive" sense is necessary in such an activity. What is the role of the teacher in such an activity? What is the role of the child?
To return to the previous page use your browser's back button.