Thoughts on Teaching Permutations, Combinations
and the Binomial
Theorem
Penelope Nom
Permutations:
First introduce n! as the number of ways of lining up n people: There are n choices for the first spot, (n-1) choices for the second, (n-2) choices for the third, and so on giving n(n-1)(n-2) ... (3)(2)(1) = n! in all.
Emphasize how fast n! grows. It actually grows similar to n^n. (We use m^n to denote m to the nth power.) For example have the students guess how long it would take for us to run through forming all the possible queues of 20 people if we could form a new queue every second. (It actually takes billions of years. Usually very few students will have any idea of how long it will take and probably will have to work it out to believe it.) This type of exponential growth obviously makes it very important to avoid factorial numbers of steps in computer algorithms, etc.
(The notations for permutations and combinations vary quite a bit, for example
with combinations we often see both
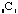 and
and
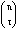 ;
certainly the latter should be used somewhat as it is almost a universal symbol
for combinations and is used particularly often when discussing the binomial
theorem.) In the present medium we are somewhat restricted in the use of
graphics and thus we will frequently use [n]P[r] and [n]C[r] to denote the
number of permutations, respectively combinations, taken r at a time. For
clarity and emphasis we will often use an * to denote multiplication.
;
certainly the latter should be used somewhat as it is almost a universal symbol
for combinations and is used particularly often when discussing the binomial
theorem.) In the present medium we are somewhat restricted in the use of
graphics and thus we will frequently use [n]P[r] and [n]C[r] to denote the
number of permutations, respectively combinations, taken r at a time. For
clarity and emphasis we will often use an * to denote multiplication.
After looking at permutations of n distinct objects I find it useful to introduce the number of permutations of n distinct objects taken r at a time as follows:
Suppose that n people show up at a theatre but inside the main doors there is only room for a queue of length r people between the doors and the ticket window. The number of such queues of length r can then be found by filling in the spots one at a time. There are n choices for the first spot, (n-1) for the second, ..., and finally (n-r+1) choices for the rth spot (note that after the rth spot is filled, (n-r) people remain outside so that at the previous step there were (n-r+1) people to choose from). The number of permutations of n distinct objects taken r at a time is thus
[n]P[r] = n(n-1)(n-2)...(n-r+1) which can be written as [n]P[r] = n!/(n-r)!
Try to get the students to understand the idea of forming the queue rather than 'memorizing' the formula for [n]P[r], it is then they will understand and be able to recall what the correct expression is. It should be stressed repeatedly that order is important when talking of permutations. One is lining up objects, people, whatever.
Combinations:
Combinations count the number of ways of choosing r of n distinct objects - no order is involved, just the number of ways of choosing them.
Denote the number of ways of choosing r of n distinct objects by [n]C[r]. Clearly this is an integer, but what integer? Going back to the queues inside the theatre doors, we solve this problem a second way and then equate the answers. When the n people show up at the theatre, first choose r of them to go inside to form the queue of r people. You can do this in [n]C[r] ways. Once inside these r people can be lined up in r! ways. Thus the total number of ways of forming the queues is [n]C[r] times r! However this must also be [n]P[r] as we've already seen, i.e.
[n]C[r]*r!= [n]P[r], or [n]C[r] = [n]P[r]/r!, equivalently [n]C[r]= n!/r!(n-r)!
Do a number of simple problems but try once again to have students think of combinations as the number of ways of choosing something rather than as a formula. Remind the students of the size of the factorials and that they should avoid factorials of 'large' numbers. Also, illustrate how if we know how many ways we can pick say 3 people from 20 we immediately know in how many ways we can pick 17 from 20 (equivalent to picking the 3 people we leave behind); in general we have [n]C[r] = [n]C[n-r].
A lottery problem may hit home for some of them:
In Lotto 649 what is the probability of
a) picking the winning ticket?
b) picking none of the right numbers for your ticket?
c) getting exactly one of the six numbers correct?
a) p = 1/[49]C[6] = 1/13,983,816, about a 1 in 14 million chance.
b) p =[6]C[0]*[43]C[6]/[49]C[6] = 6,096,454/13,983,816 =.4360... (we're picking 0 of 6 correct numbers and 6 of 43 wrong numbers).
c) p = [6]C[1]*[43]C[5]/[49]C[6] = 6(962,598)/13,983,816 = .4130... (we're picking 1 of 6 correct numbers and 5 of 43 wrong numbers).
Note that the chances of at most 1 correct is seen to be about .849, about 6 out of 7. I think you win $10 for three correct. What are the chances in this case? I think p is about .0177, roughly a one in 57 chance so that typically you'll spend $57 to win $10.
To illustrate the size of the numbers involved you might consider the following - suppose you always buy the same six numbers on Wednesday and Saturday, roughly 100 tickets per year. On the average that particular combination will come up once in roughly (1/2)(14,000,000)/100 = 70,000 years!
For more challenging questions using combinations you might try problems such as:
Show that [2]C[2] + [3]C[2] + [4]C[2] + ... +[999]C[2] = [1000]C[3]
To do this from straight calculations would of course be pretty annoying, if not futile. This is a good example of why these numbers should be thought of as the number of ways of counting something, not as some formula. The solution to the problem goes like this: In how many ways could we select 3 people from a line-up of 1000? Clearly this is counted by the right hand side of the given equation. Think of solving this another way. When we pick 3 people (starting from left to right), from where we must pick the last one? If the last one is in spot number three, we must have chosen 2 of the first 2 people already; if the last one is in spot number four, we must have chosen 2 of the first 3 people already; if the last one is in spot number five, we must have chosen 2 of the first 4 people already; ...; if the last one is in spot number 1000, we must have chosen 2 of the first 999 people already; in total the number of possible ways to choose our 3 people is the left hand side of the given equation. Since we have solved the problem correctly twice, the answers must be equal and we're done.
One can generalize the above problem in the obvious way to prove :
[r]C[r] + [r+1]C[r] + [r+2]C[r] + ... +[n]C[r] = [n+1]C[r+1].
Often in sections on permutations and combinations one sees questions such as: How many ways can we rearrange the letters in the word ABRACADABRA to form a new 'word'? Here a new 'word' is one that looks different.
If all the letters were distinct we would of course have 11! = 39,916,800 'words', but here they are not distinct - we have 5 A's, 2 B's, 2 R's, 1C and 1D. Thus permuting the 5 A's in 5! ways does not change the word, so we are out by a factor of 120. Similarly we are out by a factor of 2 twice for the B's and R's. In all there are only 11!/5!2!2!1!1! = 83,160 ways. A possibly more intuitive way to look at such a question is to first choose where the 5 A's can go in the 11 letter 'word', now place the 2 B's, next the 2 R's and finally the C and the D. Thus the number of 'words' is [11]C[5]*[6]C[2]*[4]C[2]*[2]C[1]*[1]C[1] = 11!/5!2!2!1!1! = 83,160. The same result as before.
Of course this generalizes in the natural way.
Another challenge: how many ways can you buy a dozen donuts from an unlimited supply of 5 types of donuts?
The key here is to think of how many ways can you line up 12 x's and 4 /'s. Why? There is a one to one correspondence between such lineups and possible purchases -- xx/xxx//xxxxxx/x corresponds to 2 of type 1, 3 of type 2, 0 of type 3, 6 of type 4 and 1 of type 5 etc. Thus we need to count the number of such lineups. Equivalently, how many 'words' can we make from 4 /'s and 12 x's? This is fairly easy as we have 16 spots to fill and 4 of them have to be chosen to be occupied by a /. Thus there are [16]C[4]*[12]C[12] = [16]C[4] = 1820 ways to buy the donuts.
What if you insist that you must purchase at least one of each type? Then the answer is only [11]C[4]*[7]C[7] = [11]C[4] ways. Why?
The above problems generalize in the obvious way to buying n objects from supplies of r types .
The Binomial Theorem:
For positive integer exponents the binomial theorem should really couched in terms of combinations. (Some teachers start off with Pascal's Triangle for the binomial coefficients - a mistake of putting the cart before the horse among other things.)
Consider (x+y)^4. If we think of this as long multiplication we first observe that from the product (x+y)(x+y)(x+y)(x+y) we will get terms such as x^4, x^3y, x^2y^2, xy^3 and y^4. How do we get x^4? By choosing 4 x's out of 4 x's to multiply, i.e. in [4]C[4] = 1 ways; How do we get x^3y? By choosing 3 x's out of 4 x's to multiply with a y from the remaining term, i.e. in [4]C[3] = 4 ways; How do we get x^2y^2? By choosing 2 x's out of 4 x's to multiply with y's from the other terms, i.e. in [4]C[2] = 6 ways; How do we get xy^3? By choosing 1 x out of 4 x's to multiply with y's from the other terms, i.e. in [4]C[1] =4 ways; How do we get y^4? By choosing 0 x's out of 4 x's to multiply with y's from the other term, i.e. in [4]C[0] = 1 ways. In summary we have
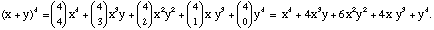
In general to find the coefficient of x^k*y^(n-k) in (x+y)^k it is simply the number of ways of choosing k x's from n x's. i.e. [n]C[k], (these k x's will be combined with y's from the remaining terms), thus we have the
Binomial Theorem for n a positive integer:
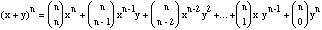 .
.
Introduce the binomial theorem this way and then have students do (x+y), (x+y)^2, (x+y)^3, (x+y)^4, (x+y)^5, (x+y)^6 etc., so as to see the pattern of coefficients. Now show them Pascal's triangle.
Have students try to deduce Pascal's Identity upon which the triangle is based, namely [n]C[r] = [n-1]C[r] + [n-1]C[r-1]. One simple way is to consider a bus trip for a class of n students. The bus can only handle r students. Also, one of the n students happens to have measles. The number of ways to fill up the bus is of course [n]C[r]. On the other hand, we must do one of two things -- leave the measly child behind or take the measly child. In the first case we must pick r people from n-1 while in the second case we must pick r-1 from n-1. Having correctly solved the problem twice, the answers must be equal giving us Pascal's Identity as required. Illustrate the construction of Pascal's triangle from this Identity.
As a challenge you might ask your students to generalize Pascal's Identity to prove:
[n]C[r] = [2]C[0]*[n-2]C[r] + [2]C[1]*[n-2]C[r-1]+[2]C[2]*[n-2]C[r-2].
(This time think of measles and malaria.)
There are many interesting properties of the binomial coefficients that can be observed from Pascal's Triangle. For example if one sums across a row they will find that they always get a power of 2. If one alternately adds and subtracts as they go across a row they find the sum is always zero. That is for the nth row of the triangle one finds
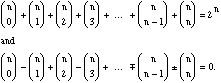
These can be proved by setting x = y = 1 and x=1, y = -1 respectively in the Binomial Theorem.
The above identities have applications when discussing sets.
If we ask how many subsets there are in a set of n elements, the first identity above counts the number of subsets of size 0, of size 1, ... , of size n, giving a total of 2^n. The second identity can be used to prove that the number of subsets with a even number of elements is equal to the number of subsets with an odd number of elements -- not at all an obvious fact, particularly when n is even.
To return to the previous page use your browser's back button.