Take a look at these four problems:

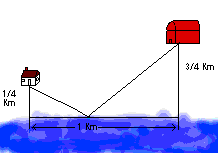
A farmer wants to walk at a constant rate from her barn to a straight river , fill her pail and carry it to her house in the least time. Determine where the farmer should fill her pail if her house and barn are located as in the diagram below:{3/4}

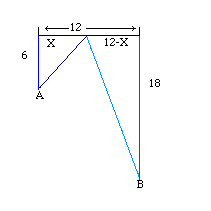
A ship is docked 6 kms from shore and opposite a point 12 kms farther along the shore another ship B is docked 18 kms offshore. A boat from the first ship is to land a passenger and then proceed to the other ship. What is the value of x so that the ship will take the shortest route. {3}

Two towns , located on the same side of a straight river agree to construct a pumping station and filtering plant at the waters edge to be used jointly to supply the towns with water. If the distances of the two towns from the river are a and b and the distances between them is c, show that the sum of the lengths of the pipe lines joining them to the pumping station is at least a great as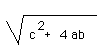

Two friends live on opposite sides of a straight river that is 100 meters wide. Mark's house is 75 meters from the river and 500 meters downriver from Tom's house. Tom's house is 300 meters from the edge of the river. A foot bridge is to be built crossing the river and perpendicular to the flow. Where should it be built in order to minimize walking distance between the house? {725}

These look like standard max-min problems for calculus. However, they do not have to be of that type. Look at this problem, how it was solved and REFLECT on the above questions.

The coordinates of A, B, and C are (7,4),(3,1) and (0,K) respectively. Find the value of K such that |AC| + |BC| is a minimum.

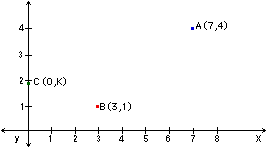
If we reflect the point (7,4) about the y -axis, the question is equivalent to minimizing |A'C| + |BC| where A' is the ordered pair (-7,4).

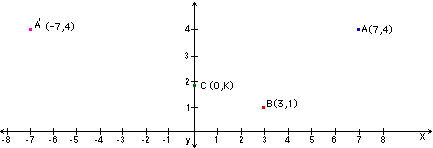
|A'C| + |BC| is minimized when C is on the line segment A'B.

Finding K amounts to solving two similar triangles.

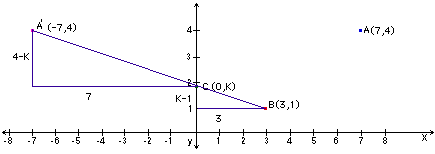
Although these are typical calculus max-min problems, a little reflection leads to a solution that does not involve calculus.