Lets look at a small example. Suppose three classes of 5 students each write the same exam and the grades are:
| Class 1 | Class 2 | Class 3 |
|---|---|---|
| 82 | 82 | 67 |
| 78 | 82 | 66 |
| 70 | 82 | 66 |
| 58 | 42 | 66 |
| 42 | 42 | 65 |
Each of these classes has a mean,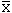 , of 66 and yet there
is great difference in the variation of the grades in each class. One measure of
the variation is the range, which is the difference between the highest and
lowest grades. In this example the range for the first two classes is 82 - 42 =
40 while the range for the third class is 67 - 65 = 2. The range is not a very
good measure of variation here as classes 1 and 2 have the same range yet their
variation seems to be quite different. One way to see this variation is to
notice that in class 3 all the grades are very close to the mean, in class 1 some of the
grades are close to the mean and some are far away and in class 2 all of the
grades are a long way from the mean. It is this concept that leads to the
definition of the standard deviation.
, of 66 and yet there
is great difference in the variation of the grades in each class. One measure of
the variation is the range, which is the difference between the highest and
lowest grades. In this example the range for the first two classes is 82 - 42 =
40 while the range for the third class is 67 - 65 = 2. The range is not a very
good measure of variation here as classes 1 and 2 have the same range yet their
variation seems to be quite different. One way to see this variation is to
notice that in class 3 all the grades are very close to the mean, in class 1 some of the
grades are close to the mean and some are far away and in class 2 all of the
grades are a long way from the mean. It is this concept that leads to the
definition of the standard deviation.
Lets look at class 1. For each student calculate the difference between the students grade and the mean.
| Class 1 | 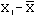 |
|---|---|
| 82 | 16 |
| 78 | 12 |
| 70 | 4 |
| 58 | -8 |
| 42 | -24 |
The average of these differences could now be calculated as a measure of the
variation, but this is zero. What is really needed is the distance from each
grade to the mean not the difference. You could take the absolute value of
each difference and then calculate the mean. This is called the mean deviation, i.e.
mean deviation = 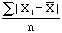 , where n is the number of
students in the class. For class 1 this is 64/5 = 12.8. Another way to deal
with the negative differences is to square each difference before adding.
, where n is the number of
students in the class. For class 1 this is 64/5 = 12.8. Another way to deal
with the negative differences is to square each difference before adding.
| Class 1 | 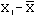 |
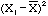 |
|---|---|---|
| 82 | 16 | 256 |
| 78 | 12 | 144 |
| 70 | 4 | 16 |
| 58 | -8 | 64 |
| 42 | -24 | 576 |
The sum of this column is 1056. To find what is called the standard deviation,
s, divide this sum by n-1 and then, since the sum is in square units, take the square root.
For class 1 this gives 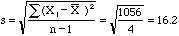
A similar calculation gives a standard deviation of 21.9 for class 2 and 0.7 for class 3. So for class 3, where the grades are all close to the mean, the standard deviation is quite small, for class 1, where the grades are spread out between 42 and 82, the standard deviation is considerably larger and for class 2, where all the grades are far from the mean, the standard deviation is larger still. The standard deviation is the quantity most commonly used by statisticians to measure the variation in a data set.
The reason that the denominator in the calculation of s is n-1 deserves a
comment. To look at this lets change the example. Suppose that I am interested
in the number of hours per day that high school students in North America spend
doing their mathematics homework. The "population" of interest is all high
school students in North America, a very large number of people. Lets call this
number N. My real interest is the mean and standard deviation of this
population. When talking about a population statisticians usually use Greek
letters to designate these quantities, so the mean of the population is written
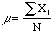 , (
, (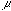 is the Greek
letter mu). Likewise the standard deviation is
is the Greek
letter mu). Likewise the standard deviation is 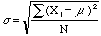 , (
, (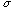 is the Greek letter sigma). Notice that
here the denomonator in the calculation is N.
is the Greek letter sigma). Notice that
here the denomonator in the calculation is N.
Rather than trying to deal
with this large population a statistician would usually select a "sample" of
students, say n of them, and perform calculations on this smaller data set to
estimate mu and sigma. Here n might be 25 or 30 or 100 or maybe even 1000, but
certainly much smaller than N. To estimate mu it seems natural to use 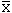 , the mean of the sample. Likewise to estimate sigma it seems
reasonable to use
, the mean of the sample. Likewise to estimate sigma it seems
reasonable to use 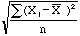 , but this quantity
tends to underestimate sigma, particularly for small n. For this and other
technical reasons the quantity
, but this quantity
tends to underestimate sigma, particularly for small n. For this and other
technical reasons the quantity 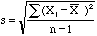 is a
usually preferred as the estimator to use for sigma.
is a
usually preferred as the estimator to use for sigma.
If you have a calculator that computes the standard deviation it is a good exercise to see if it divides by n or n-1. Take the three number data set -1,0,1, calculate the standard deviation both ways by hand and then use your calculator to see which method it uses.
Footnote:In the Spring of 2000 I received a request by a teacher to elaborate on the reasons why statisticians divide by n - 1 when calculating the sample variance. My reply was to describe an experiment that he could have his students perform in the classroom.
Harley
Footnote:
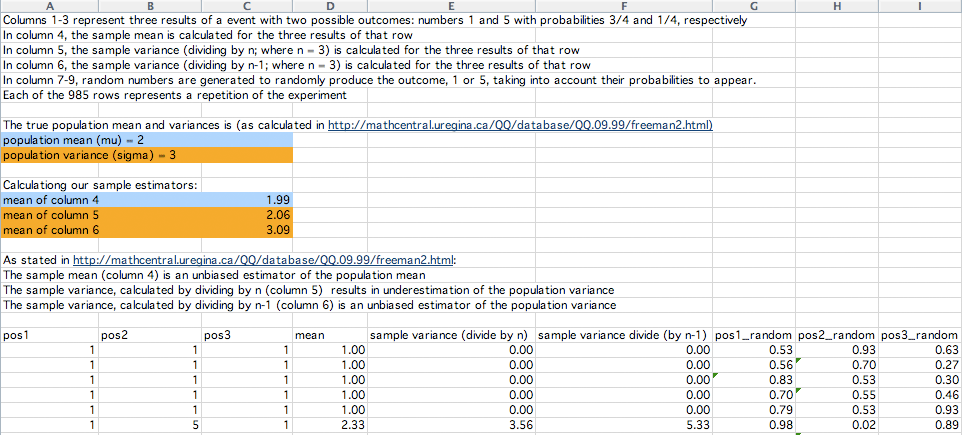
In December 2009 Javier Quílez Oliete, a doctoral student in Barcelona Spain, sent an Excel file where he simulated the experiment that I suggested in the previous footnote. He simulates repeatedly selecting a sample of size 3, with replacement, from a set with the two numbers 1 and 5 where the probability of selecting the 1 is 3/4 and the probability of selecting the 5 is 1/4. His simulation has 985 repetitions and for each of the 985 samples of size n = 3 he calculates the sample mean, the sample variance dividing by n, and the sample variance dividing by n - 1. He then compares these sample statistics to the population mean and variance.
Below is a snapshot of the first few lines of Janvier's spreadsheet. Click here to download Javier's spreadsheet.
Thanks Javier,
Harley
To return to the previous page use your browser's back button.