Measurement,
Perimeter
& Area

Grade 7, 8, 9
By
Greg Brososky
Fairview Middle School
Swift Current, Saskatchewan
&
Michael Neufeld
Rabbit Lake Central School
Rabbit Lake, Saskatchewan
1994
EDITOR'S NOTE:
The following abbreviations are used for the Common Essential Learnings (CELs).
- Communication - C
- Critical and Creative Thinking - CCT
- Numeracy - N
- Personal and Social Values and Skills - PSVS
- Independent Learning -IL
- Technological Literacy - TL
I. TOPIC: LINEAR MEASUREMENT
II. FOUNDATIONAL OBJECTIVES:
The student should demonstrate:
- a sense of spatial awareness and familiarity with two- and three-dimensional
shapes and recognize relationships between geometry and the environment;
- an ability to measure and use appropriate measurement techniques and to
apply
measurement to real life;
III. SPECIFIC LEARNING OBJECTIVES:
The student should be able to:
- solve a variety of problems involving length
- compare, estimate, then measure and record lengths/distances
- recognize and use the appropriate unit of measure length or distance given a
real world measurement situation
- understand the relationships between kilometres, metres, decimetres,
centimetres and millimetres
- convert metric units of length
IV. STRATEGIES:
- Interactive Instruction
- Independent Learning
- Experiential Learning
V. METHODS:
- Peer Practice
- Research project
- Field Observations
- Co-operative Learning
VI. DESCRIPTION:
A.
Students construct a "Personal Data Sheet" containing individual
body measurements. Students can use cloth tapes and work in groups or in
pairs. Room can be left on the card for students to add other measurements
suggested by the teacher.
PERSONAL DATA SHEET
| Height | ____cm |
|---|
| Finger tip to finger tip | ____cm |
|---|
| Top of head to chin | ____cm |
|---|
| Top of head to eyes | ____cm |
|---|
| Around neck | ____cm |
|---|
| Around bisceps | ____cm |
|---|
| Length of foot | ____cm |
|---|
| Elbow to wrist | ____cm |
|---|
Students may find it interesting to explore the ratios between the various
measurements.
B.
Scavenger hunt. Students are given a list of objects to
measure both
within the school and the classroom and outside the school. Groups are
supplied with record sheets, tape measures and trundle wheels. The results can
be shared, not so much to ensure accuracy as to ensure the use of appropriate
units.
C.
To reinforce the metric ladder conversion method, large
colorful signs
can be constructed. Place these signs on a staircase and having students move
from one step to another while announcing the change in the original value.
Students gain a working knowledge of how the ladder is used to convert metric
units.
VII. ASSESSMENT TECHNIQUES:
Performance Assessment:
(samples provided in appendix)
- rating scale
- observation checklist
- anecdotal records
Written Assignments:
- contracts
- self and peer assessments
VIII. CELs:
Students should develop their abilities to:
- discover relationships and patterns, propose generalizations that
explain the
relationships, and apply the conclusions and generalizations to new situations
(CCT);
- understand the benefits and limitations of measuring tools and calculating
devices and use technological innovations as helpful learning tools (TL);
- work cooperatively, contribute positively in group learning activities and
treat with respect themselves, others and the learning materials used (PSVS)
I. TOPIC: PERIMETER
II. FOUNDATIONAL OBJECTIVES:
The student should demonstrate:
- a sense of spatial awareness and familiarity with two- and three-dimensional
shapes and recognize relationships between geometry and the environment:
- an ability to measure and use appropriate measurement techniques and to
apply
measurement to real life;
III. SPECIFIC LEARNING OBJECTIVES:
The student should be able to:
- compare, estimate, then measure and record lengths/distances
- locate and calculate the perimeter of regular polygons, irregular polygons
and composite figures
- calculate the perimeter of a figure given the a) length of all sides and b)
partial, but sufficient information
- explore the relationship between the radius, diameter and the circumference
of a circle
- find the radius or diameter of a circle, given the circumference
IV. STRATEGIES:
- Independent Learning
- Experiential Learning
V. METHODS:
- Learning Activity Package
- Model Building
- Field Observations
VI. DESCRIPTION:
A.
Have students, perhaps during art classes, construct mobiles out
of coat hangers or other wire. The shapes could vary. All, or selected ones,
could be hung from the ceiling to act as a reminder and reference when the
topic changes to area.
B.
Students are given geo-boards and asked to construct shapes
with given
perimeters. There may be a variety of correct answers depending upon the number
chosen for the perimeter. Students can exchange their work and examine the
variety of shapes constructed. Discuss the various figures created. Encourage
the use of shapes with 90 degree angles or be prepared to handle questions that
arise regarding sloping distances. This limits it to rectangles or squares.
C.
Have students cut out a square, 25 cm. X 25 cm., and find the
perimeter of
the square. Have them cut another square, 10 cm. X 10 cm., from the top right
corner of the first square. Have them find the perimeter of the new shape
formed when the smaller square is removed. Ask the students to cut out other
squares of their choice and cut from the top right corner, squares of different
sizes. Have them find the perimeter. Ask students to list any observations
that they see. Note that the loss of the area as the square removed does not
affect the perimeter. This should point out that perimeter is not related to
the area of the figure.
D.
Students use string, cloth tape and/or a trundle wheel to
measure the
circumference of various circles (cup, can, barrels, jump circle in gym etc.).
They also record the diameter of the circles. This information can be recorded
in a chart which when brought back to the class can be shared using a chart on
the board. Students are asked to determine the relationship between the two to
gain an understanding of the value of pi and it role in the formula for the
circumference of a circle.
E.
Students cut circles out of paper. (Encourage students to
use circles
with diameters which are whole numbers....this will make the connection between
diameter and area more easily observed.) They then cut the circles in half by
cutting along the diameter. Each half is then cut into small slices running
from the circles center to the outside edge. When finished the edges of the
circle are laid side by side and measured to arrive at an approximation of the
circumference.
VI. ASSESSMENT:
Performance Assessment:
- assessment station
- data collection checklist
- anecdotal records
- self assessment
Written Assignments:
- contracts
- portfolios
- rating scales
VII. CELs:
Students should develop their abilities to:
- show their understanding of ideas presented by providing an alternate
rephrasing, drawing a diagram, making a model, etc. (C);
- understand the benefits and limitations of measuring tools and calculating
devices and use technological innovations as helpful learning tools (TL);
- work cooperatively, contribute positively in group learning activities and
treat themselves, others and the environment with respect (PSVS);
I. TOPIC: AREA
II. FOUNDATIONAL OBJECTIVES:
The student should demonstrate:
- a sense of spatial awareness and familiarity with two- and three-dimensional
shapes and recognize relationships between geometry and the environment:
- an ability to measure and use appropriate measurement techniques and to
apply
measurement to real life;
III. SPECIFIC LEARNING OBJECTIVES:
Students should develop their abilities to:
- solve a variety of problems involving area
- compare, estimate and then measure the area of regions using square
centimetres and square metres
- discuss the relationships between the length, width and area of a rectangle
(including squares)
- estimate and find the area (using a formula) of squares, rectangles,
triangles, parallelograms, rhombuses, trapezoids, composite figures and
circles
IV. STRATEGIES:
- Experiential Learning
- Direct Instruction
- Interactive (from chart)
V. METHODS:
- Model Building
- Demonstration
- Cooperative Learning
VI. DESCRIPTION:
A.
Have students, perhaps during art classes, cut flat shapes out of
cardboard. These shapes would be covered with paper mâché and
painted with bright acrylic paint. Coating the shapes with varnish will add to
their visual impact. All, or selected ones could be hung in a region of the
room (perhaps hung from the ceiling) to act as visual reference. If done in
conjunction with the coat hanger mobiles, it will make a valuable contrast
between the two concepts. Formulae could be attached to the side of each
shape. A variety of shapes (triangles, rectangles, parallelograms) should be
displayed.
B.
Students are given geo-boards. Students are asked to create
shapes with
various given areas. Students chart the length and width of the shapes as
well as the perimeter along with the area that was given to them. Students can
be asked to draw conclusions about the relationship between the length, width
and the area. Relationships between area and perimeter can also be discussed.
This same activity could be accomplished with building cubes (base ten
blocks).
C.
Students cut out rectangles and then calculate and record the
area using
the formula. A sloping vertical line is drawn across the rectangle. Students
cut along this line dividing the shape in two. The right and left sides are
reversed creating a parallelogram. The area has not changed. Students record
the dimensions of the new shape. During the discussion that follows students
should be led to the understanding that a new formula (not LxW) is required to
find the area of the parallelogram, and that base and height are now more
appropriate.
D.
Students cut parallelograms out of squared paper. The
parallelogram is cut
into triangles. Both the areas of the parallelogram and the triangles are
recorded (use formula for the parallelogram and counting for the triangle). By
using different methods, students may arrive at slightly different answers.
Students share their results in a chart on the board and are led to the
conclusion that the areas of the triangles are half of the area of the original
parallelogram and thus to the formula for the area of the triangle.
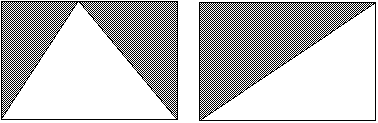
E.
To help students better understand the method of calculating the area of
rectangular shapes, have the students draw the images on grid paper. Students
can then cut out the shapes, calculate the area of individual areas and then
paste them together again. The total area is then seen to be the total of the
individual areas.
F.
Students are given a sheet of grid paper containing an
irregular polygon.
They calculate the area and the perimeter. Students are then asked to draw a
shape on a second sheet of grid paper where the perimeter remains the same but
the area is the largest possible. Similarly, with the same perimeter but the
smallest area possible. Calculating the area of an irregular polygon could be
interesting. How might they do this? Geoboards, or by counting or dividing into
triangles, calculations and sums? Their written description of the process
might be worthwhile.
G.
Each student is given an orange (or other round edible
item...ie pizza,
bannock) and asked to record dimensions associated with the item (see chart
below). Cut a slice about one centimetre thick from the center of an orange.
Lay the slice on a piece of paper. Measure and record the radius of the slice.
Cut the slice in half. Separate the sections in each half. This can be done
easily if the students did not cut through any of the triangular sections
inside the orange. Arrange the sections as shown below. Use the formula for
the area of a parallelogram to calculate the area of the constructed shape.
Student results are recorded on the board and students, through trial and error
are encouraged to determine any relationships between the various elements.
After much foraging students will see the constant connection (pi) between the
area and the radius. An alternate method would be to have students work in
groups to arrive at an appropriate formula and then present their findings to
the rest of the class.

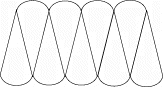
H.
Papers containing the following shapes are distributed to
the students.
Either individually or in groups, the students calculate the area of the white
regions in each dark square and the dark area surrounding them. This should
give the student experience in subtracting to arrive at the area of a specific
region. The results showing the areas to be the same in each of the squares
will be very interesting.

VI. ASSESSMENT
(samples provided in appendix):
- Performance Assessment:
- ancecdotal records
- observation checklist
- Written Assignments:
- portfolios
- observation checklist
- Presentations
- anecdotal records
- observation checklist
VII. CELs:
Students should develop their abilities to:
- show their understanding of ideas presented by providing an alternate
rephrasing, drawing a diagram, making a model, etc. (C);
- discover relationships and patterns, propose generalizations that
explain the
relationships, and apply the conclusions and generalizations to new situations
(CCT);
REFERENCES:
A Teacher's Guide to Math Works, Agency for Instructional
Technology, 1985
Daily Mathematics, Critical Thinking and Problem Solving, McDougal,
Littel & Co.
Intermediate Math 1, Dottori D., Knill G., et. al., McGraw-Hill Ryerson
Ltd., 1981
Math In Context, Ebos F., McKillop D., et. al., Nelson Canada, 1992
Math Quest, Alexander B., Folk S., & Worth J., Addison-Wesley
Publisher, Ltd., 1989
Checklist to Assess Student's Ability to Use Information
Student Name:_______________________________________________
Date or Time Period of
Assessment:_________________________________________________
Check all applicable criteria.
| Criteria | Yes/No |
|---|
1. Student is able to state the purpose for
the collection of the information. |
_______ |
2. Student is able to gather information from
own recall of past learning. |
_______ |
3. Student is able to identify main elements
needed in information. |
_______ |
4. Student is able to organize information
into usable units. |
_______ |
5. Student is able to identify related details. |
_______ |
6. Student is able to recognize relationship
of information gathered to information
remembered. |
_______ |
7. Students is able to clearly state ideas that
fit with the topic being addressed. |
_______ |
8. Student is able to give evidence of checking
information for accuracy. |
_______ |
(This instrument may be adapted
for use as a rating scale.)
Student Evaluation Handbook, 1991
The following rating scale could be used to record observations of a group
involved in a collaborative project. Teachers could use this scale to describe
each student's contribution to the group and the development of co-operative
skills.
Co-operative Group Learning (Teacher Assessment)
Date:_______________________________________________
Group:______________________________________________
Task:________________________________________________
5 4 3 2 1
High Low
|
Names of Group Members
|
| ________ |
________ |
________ |
________ |
________ |
________ |
|
|
|
Negotiates roles and responsibilites of each group member |
___ |
___ |
___ |
___ |
___ |
___ |
|
Contributes ideas and suggestions |
___ |
___ |
___ |
___ |
___ |
___ |
|
Encourages the involvment of all group members |
___ |
___ |
___ |
___ |
___ |
___ |
|
Is receptive to peer questions and criticism |
___ |
___ |
___ |
___ |
___ |
___ |
|
Listens to the suggestions of others |
___ |
___ |
___ |
___ |
___ |
___ |
|
Modifies personal thinking to incorporate the ideas of others or new
information |
___ |
___ |
___ |
___ |
___ |
___ |
|
Respects and accepts the contributions of each group member |
___ |
___ |
___ |
___ |
___ |
___ |
|
Completes individual commitment to the group |
___ |
___ |
___ |
___ |
___ |
___ |
Additional Comments:
__________________________________________________
__________________________________________________
__________________________________________________
__________________________________________________
__________________________________________________
__________________________________________________
English Language Arts
A Curriculum Guide for the Elementary Level
June 1992, Saskatchewan Education
Students could discuss questions such as the following to assess the group's
ability to work co-operatively.
Co-operative Group Learning (Group Assessment)
1. Was your group successful in working together? What co-operative
skills did the group use to make working together enjoyable?
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
2. What co-operative skills improved as the group project progressed?
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
3. What co-operative skills need to be further developed?
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
4. What was the most important thing your group learned about working together
during this project?
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
English Language Arts
A Curriculum Guide for the Elementary Level
June 1992, Saskatchewan Education
Assessment of Cooperative Learning
~ Individual ~ Pair ~ Group
Student Name:_____________________________________
Partner/Group Members:_____________________________
_________________________________________________
_________________________________________________
_________________________________________________
Date:____________
DIRECTIONS:
Please meet with your group and use the rating scale below as a basis for
discussing how effectively your group is working. Complete the rating scale and
return it to your instructor.
DID YOUR GROUP: |
POORLY........................................EXTREMELY
WELL
|
-
Identify specific goals?
|
1 2 3 4 5 6 |
-
Make noticeable progress towards those goals?
|
1 2 3 4 5 6 |
-
Share information, ideas, and opinions with each other?
|
1 2 3 4 5 6 |
-
Make decisions that were based on the views of all members?
|
1 2 3 4 5 6 |
-
Listen with attention to each other?
|
1 2 3 4 5 6 |
-
Actively encourage each other to participate in the group activities?
1 2 3 4 5 6 | |
Some suggestions for improving our group work next time:
________________________________________________
________________________________________________
________________________________________________
________________________________________________
>From Business Education Accounting 16, 26, 36
Saskatchewan Education 1992
Student Evaluation: A Teacher Handbook, 1993
Rating Scale for Cooperative Group Learning
Student Name:________________________
Date or Time Period of Assessment:____________________
1. The student works with a wide range
of peers, not just with close friends. |
1 2 3 4 5
never sometimes always |
2. The student willingly shares materials
and ideas with others. |
1 2 3 4 5
never sometimes always |
3. In group work the student shows
respect for others by listening and
considering other points of view. |
1 2 3 4 5
never sometimes always |
4. The student follows group work
rules as established for the activity. |
1 2 3 4 5
never sometimes always |
5. The student fulfills her/his work
responsibilities in the group. |
1 2 3 4 5
never sometimes always |
6. The student exhibits appropriate work
behaviors during time set aside for groups. |
1 2 3 4 5
never sometimes always |
7. The student participates in discussions
during the time set aside for group work. |
1 2 3 4 5
never sometimes always |
8. The student contributes ideas to
the group efforts during the
discussions in the time set aside for
group work. |
1 2 3 4 5
never sometimes always |
This instrument may be adapted for use as a checklist.
Student Evaluation Handbook, 1991
Anecdotal Record
Student Name:_________________________
Class:________________________________
Term:________________________________
After an anecdotal notion is written on a pre-pasted note, the teacher may add
it to this anecdotal record sheet. The teacher will circle the focus for each
anecdotal entry.
Date: __________________________________
Focus: Knowledge Application Technical Skills Attitude
Date: __________________________________
Focus: Knowledge Application Technical Skills Attitude
Date: __________________________________
Focus: Knowledge Application Technical Skills Attitude
|
From
Business Education Accounting 16, 26, 36
Saskatchewan Education 1992
Student Evaluation: A Teacher Handbook, 1993
Template 1
Anecdotal Record-Keeping Form
Date:_________________________
Unit:_________________________
Student's Names
|
Criteria/Objectives
|
|---|
| | td>
|
|
|
|
|
|
|
|
|
|
Special Comments:
________________________________________________
________________________________________________
________________________________________________
________________________________________________
Student Evaluation: A Teacher Handbook, 1993
Arts Education
A Curriculum Guide for Grade 1
September, 1991, Saskatchewan Education
Data Collection/Notebook Checklist*
Name:_________________________
Date:__________________________
A checkmark indicates that the criterion is satisfactory. No mark
indicates that the criterion is either missing or unsatisfactory.
- Documentation is complete.
|
|
- The information or data collected is accurate.
|
|
- Written work is neat and legible.
|
|
- Tables and diagrams are completed neatly.
|
|
- Each new section begins with an appropriate heading.
|
|
- Errors are crossed out but not erased.
|
|
- Spelling and language usage are edited and corrected.
|
|
- Information is recorded in a logical sequence.
|
|
- Technological aids are used appropriately.
|
|
- Notes are collected in a folder or binder.
|
|
- Color or graphics are used to enhance the appearance.
|
|
- Rough work is done separately.
|
|
Comments/Overall Impressions:
________________________________________________
________________________________________________
________________________________________________
________________________________________________
* This checklist may be used by teachers, or by students for self-evaluation.
It may be used to evaluate notebooks, laboratory data collection done during
investigations, or more formal written laboratory reports. Students should be
made aware of these criteria at the start of the term.
Student Evaluation: A Teacher Handbook, 1993
Science
A Curriculum Guide for the Secondary Level
September, 1991, Saskatchewan Education
This unit comes from the The Stewart Resources Centre which provides
library resources and teacher-prepared materials for teachers in Saskatchewan.
To borrow materials or obtain a free catalogue listing unit and lesson
plans contact :
Stewart Resources Centre,
Sask. Teachers' Federation,
2317 Arlington Avenue,
Saskatoon, SK S7J 2H8;
phone 306-373-1660; fax 306-374-1122,
e-mail src@stf.sk.ca.
http://www.stf.sk.ca/
Go to Math Central
To return to the previous page use your browser's back button.





