Intoduction to

for Middle Years Mathematics

Table of Contents

• Analytic Geometry
  
  
• Lesson 1: Plotting Points on a Cartesian Grid using the Geoboard
  
  
• Lesson 2: Graphing Lines on the Cartesian Grid
  
  
• Lesson 3: Determining the Slope and Y-Intercept of the Line
  
  
• Lesson 4: Determining the Slope Using Coordinate Points
  
  
• Lesson 5: Parallel and Intersecting Lines in Relation to Slope
  
  
• Open Book Quiz
  

Precis:
This topic deals with the Cartesian grid and linear equations with some analysis of the graph of the line and its relationship to the equation of the line. This topic was completed in five - fifty minute periods.

I. BACKGROUND

• point, line, line segment Grade 3/4
  
• parallel, intersecting and perpendicular lines Grade 5
  

II. RESOURCES

• geoboard
  
• TI-81 Emulator Program (Macintosh Computer)
  
• coordinate grid (I used a coordinate grid which was a Clarisworks creation by Jonathan Elder, a Grade Eleven student at Fillmore)
  

III. SEQUENCE

• Grid Systems - examples
  
• Grid
  
• Locating Coordinates
  
  • examples
  • geoboard

Relations:
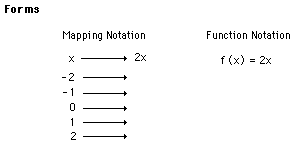
Forms

• Mapping Notation
  
• Function Notation
  
• Equations of Lines
y = 2x, y = 3x, y = -2x, y = -3x with x, y charts.

• geoboard
  
• computer (TI-81 Emulator program)

Slopes of Lines
Use equations
y = 2x
y = 3x
y = -2x
y = -3x
to explain m = (rise)/(run)

• use y-intercept as a starting point
  
• positive, negative Ü horizontal and vertical and vertical slopes will be covered ater.
  
  y = + mx
  
  y = + mx + b (slope-y-intercept equation)
  Ax + By = C
  
  
  

  Calculating slopes using coordinates.
  m = y2 - y1
  
  x2 - x1

  Horizontal and Vertical Lines
  
  Parallel Lines-equations of lines used to illustrate the relationship between slope and parallel lines.
  
  Intersecting Lines-equations of lines were used to indicate the relationship between slope and intersecting lines.

The students were instructed on use of the Emulator program and were to, with supervision, key in a couple of equations to graph. This topic took 4.5 classes of instruction with 0.5 of a class for an OPEN BOOK QUIZ.

IV. STUDENT MATERIALS

• Graph Paper
• Straight-Edge
• Notebook

V. CELs

1. Communication
2. Creative and Critical Thinking
3. Numeracy
4. Technological Literacy

VI. LESSONS

• with assignments
• instructional methods
• classroom management techniques

Learning Objective

Cartesian Coordinate Grid (Descartes)

1. Grid Systems
   
   • grid road maps - Saskatchewan
     
   • township maps or the local Rural Municipality Map
     
   • games - battleship
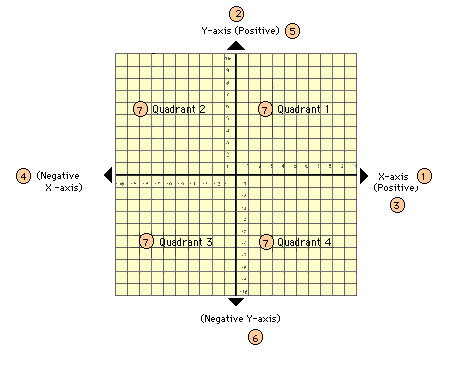
2. Grid

   Key:
   1. x axis
   2. y axis
   3. positive x
   4 negative x
   5. positive y
   6. negative y
   7. quadrant 1, 2, 3, 4

   

   
   

3. Locating Coordinates
   
   
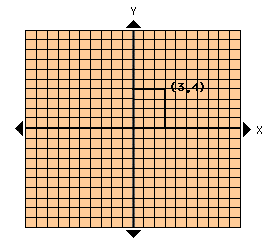
   • example: (3,4)------ (x,y)
     
     
4. Geoboard
   
   • coordinate search (5 minutes)
     
   • given points A-K (oral correction with instructor writing correct answer on blackboard)
     
   • the instructor has previously placed the points on the geoboard using a nonpermanent marker

Interactive

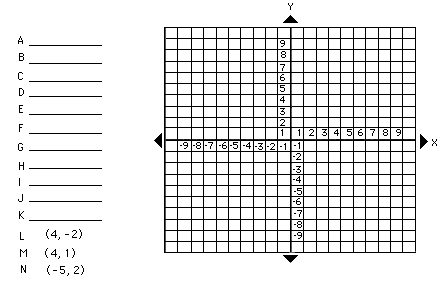
• plot 3 points L, M, N Ü hand out nonpermanent markers and when students are finished, take them back in.

Relations

• a comparison of numbers: from newspapers, etc.
  

Equations of Lines (results will be as ordered pairs with x, y elements of the set of integers)

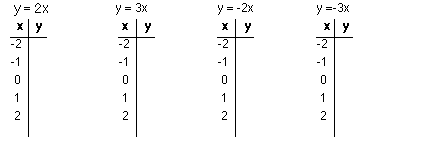
Results will be ordered pairs as (x,y), with x, y elements of the set of integers

ASSIGNMENT 1

• Plot points on graph paper (different grids)
  
• Label graph using equation.

Learning Objective

• The students will be able to graph line on a Cartesian coordinate grid.
  
• The students will be able to determine the slope and y-intercept of the line given:
  • the graph of the line
    
  • the equation in slope - y-intercept form
    

Indirect Instruction: reflective discussion on x, y charts using the set of integers.

Correct Assignment One

• examine relationships between equation
  
  • positive and negative directions
    
  • origin

Direct Instruction: compare and contrast; demonstration

• use same equations where x y R
  
  • geoboards - four elastics the students appreciated the use of the geoboards as it gave them an idea of the rise and the run.
    
  • TI-81 Mac Emulator program
    
  • brainstorm with students various examples of lines used in architecture, house design, natural landscapes (ski slopes), engineering designs Ü to develop an intuitive idea of the applications of lines.

Slope

• Use equations from assignment 1 where x and y are real numbers.

• Slope
  
  • y-intercept equation: y = ± mx
    
  • use assignment 1 equations as examples.
    
  • the y-intercept is the origin.

• Slope
  
  
  • y-intercept equation: y = ± mx + b
    
  • the y-intercept is not the origin.
    
  • TI-81 Emulator program: y = mx + b
    
    
    • instructor will key in sets of equations to illustrate different equations
      
  
  
• the use of the TI-81 Emulator program by the students was somewhat reserved and they did not really understand the connection between the equation y = mx + b and the graph of the equation. This was corrected by some direct instruction on the blackboard and a paper and pencil assignment similar to the following:

SET 1:
a) y = x + 1
b) y = x - 1
c) y = -x + 1
d) y = -x - 1
examine similarities and differences.

SET 2:
a) y = 2x - 1
b) y = 2x - 3
c) y = 2x + 1
d) y = 2x - 3
examine similarities and differences.

Learning Objective

• the graph of the line (review)
  
• the equation in slope-y-intercept form (review)
  
• the equation in standard form

Independent Learning: computer assisted instruction

• Supervise students computer use - 0.5 hour
  
• Geoboard: use to illustrate the determination of slope using the y-intercept as a starting point.
  
• Slope: m = RISE/RUN
  
  
  • use of elastics to determine the run from the y-intercept to the next x coordinate. Determine the rise.
• paper and pencil graphing to show how slope y-intercept graphing works, (as opposed to using an x, y chart).

Direct Instruction: structured overview and demonstration.

• Standard Form equations.
  
  
  • Ax + By = C
    
    
    • Solve for y: y = -(A/B)x + C/B
      
    • From any given equation in standard form select the numerical coefficients for A, B and C and determine slope using m = rise/run = -A/B. For the y-intercept b use C/B.

ASSIGNMENT 2

1. Determine the slope and the y-intercept of the following equations:
   

   	a) y = x 		b) y = 7x
   
   	c) y = -4x 		d) y = 2x + 7
   
   	e) y = 8x + 6 		f) y = -4x 2
   
   	g) y = -6 - 3x 		h) 2x + y = 4
   
   	i) 7x + 6y = 4 		j) 12y + 3x = 14
   
   

   
   
2. Determine the equation of the line in:
   
   • slope - intercept form
     

     	a) m = 3 and b = -2
     
     	b) m = -7 and b = 4
     
     	c) b = 1 and m = 3
     
     

     
     
   • standard form
     

     	d) -A/B = 6 and C/B = 2
     
     	e) -A/B = -3 and C/B = 2
     
     	f) -A/B = -1 and C/B = 1
     
     

The instructor and the students went through these questions as a group (except 1hij and 2def).

Learning Objective

Direct Instruction: structured overview

• Finish correcting Assignment 2
  
  
  • if any problems occur, use the geoboards or if time is a factor, use the blackboard or computer.
    
  • Calculating slopes using coordinates
    m = (y2 - y1)/(x2 - x1)
    
    
  • plot coordinates for some samples and then calculate the slope by substitution into the slope formula.

ASSIGNMENT 3

Horizontal and Vertical Lines

• the slopes of MN and OP were used to illustrate horizontal and vertical lines (graph of each was shown).
  
• several samples were given on the blackboard and equations were used to indicate connection with coordinates and equations.
  

Learning Objective

• the graphs of the lines
  
• the equations of the two lines in slope - y-intercept form.

• Parallel Lines
  
  
  • equations of lines were used to illustrate the elationship between slope and parallel lines.
• Intersecting Lines
  
  • equations of lines were used to indicate the relationship between slope and intersecting lines.

VII. SUMMARY FOR STUDENTS

VIII. EVALUATION

• QUIZ : OPEN BOOK / 20 MINUTES

The rationale for the open book nature was that this was the first visual representation of the equation of the line as it relates to the cartesian grid. GRID.

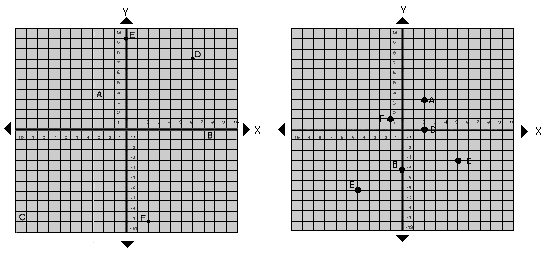
1. What are the coordinates for the points on the grid (3 marks)
(Use first graph)

A _____, B _____,

C _____, D _____,

E _____, F _____ .



2. Plot the points on the grid: (3 marks)

(Use second graph)

A(2,3); B(0,4); C(5,-3); D(2,0); E(-4,-6), F(-1,1)

3. Complete the x, y chart for the following equations: (2 marks)


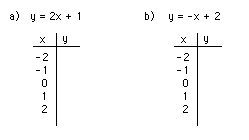
4. What is the slope for the following equations: (3 marks)
a) y = 7x - 3
b) y = -3x + 3
c) 3x + 2y = 5



5. What is the slope and y-intercept of the following equations: (4 marks)
a) y = -2x
b) y = 7x + 6


6. Determine the slope: (6 marks)
a) (-3,6) (-1,3)
b) (7,0) (2,1)
c) (0,3) (0,6)


7. For the equation sets given determine which are parallel and which intersect: (3 marks)

	a) y = 7x - 2 		b) y = 3x + 2		 c) y = x - 1


	y = -7x - 2 		y = 3x - 3 		y = x + 1