Direct and Partial
Variations
Mathematics 10
by
Ray Mah
Rossignol School
Ille à la Crosse, Saskatchewan
1993

This unit is taught upon completion of the unit on linear functions. Direct
and partial variations are applications of linear functions.
- Foundational Objective:
- To use the knowledge of linear functions and equations to solve problems
involving direct and partial variation.
- Learning Objectives:
- Curriculum Guide (p. 24)
- 19. To identify, describe, and interpret examples of direct variation
in real
world situations.
- 20. To solve proportions involving direct variation.
- 21. To solve problems involving direct variation.
- 22. To identify partial problems involving partial variation.
- 23. To solve problems involving partial variation.
- See Curriculum Guide, p. 124-127 for instructional notes, examples and ideas
for adaptive dimensions.
- References:
- Holtmath 10 c1987,
- Addison-Wesley Mathematics 10, c1987
- Math Matters 10, Nelson Canada, c1990 (Multi-text approach is
recommended)
- This is a Yes: Concept Attainment. Sheryl Mills. Saskatoon: Saskatchewan
Professional Development Unit and Saskatchewan Instructional Development and
Research Unit, 1991
- Instructional Strategies:
- (See Curriculum Guide, p. 248-250). In addition to lecturing, practice, and
drill, the following instructional strategies are very suitable:
- cooperative learning
- concept attainment (a planning form is attached)
- problem solving
- compare and contrast
- Assessment and Evaluation:
- (See Curriculum Guide, p. 9-16 and p. 73-92)
- It is recommended that a variety of methods is used. An excellent
collection
of templates for assessment and evaluation is included in the curriculum
guide.
- Objective 19:
To identify, describe, and interpret examples of direct variation
in real world
situations.
Lesson Plan:
- 1. Review of prerequisite skills
- 2. Develop working definitions of new terms
- 3. Work out some examples
- 4. Practice
|
1. Review of prerequisite skills:
- Introduce the lesson with a quick review of the definitions of relations,
functions, mapping, ordered pairs, graph of a function, etc.
2. Definitions:
- In every relation there is a variation between the two variables. When the
value of one variable changes, there is a corresponding change in the value of
the other variable. Demonstrate with familiar direct variation such as:
- distance travelled varies directly as time.
- weekly wage varies directly as hours worked.
- volume of a gas varies directly as its Kelvin temperature.
- hotel cost varies directly as the number of days.
- the expansion of a metal rod varies directly as the change in
temperature.
- the circumference of a circle varies directly as the radius
- List some relations that are not direct variations such as:
- the speed and time on a trip of 100 km
- the weight bearing capacity of beam and its length
- the force of attraction between two bodies and the distance of
separation
(NOTE: Concept attainment works well here)
3. Worked example:
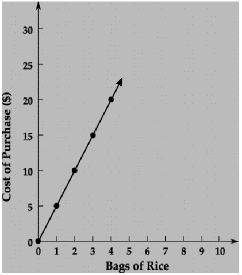
Wild rice retails at $5.00 per 500g bag. Construct a table of values relating
cost and number of bags purchased. Graph the variation. Is it a direct
variation? What is the constant of variation?
Graph of the variation |
|
|---|
|
Table of Values
|
Bags |
0 1 2 3 4 |
|---|
|
Cost $ |
0 5 10 15 20 |
|---|
| |
NOTE: Since the graph is a straight line starting at the origin, it
is a direct
variation. The constant of variation is 5. The equation of the line is y =
5x
Summary: The type of variation can be identified by the graph of the
relation. The graph of a direct variation is a straight line and starts at the
origin. The slope of the line is the constant of variation. The equation of a
direct variation is of the form y = mx, more commonly written as y = kx.
4. Practice:
- To enforce the fact that the graph of a direct variation is linear and
starts
at the origin, provide the students with an assortment of different graphs to
identify. (See page 179, Holtmath 10).
- In addition to the practice problems in math texts, direct variation
problems
can be found in physics and chemistry texts.
- Objective 20:
To solve proportions involving direct variation.
Lesson Plan:
- 1.Review of prerequisite skills
- 2.Develop working definitions of new terms and symbols
- 3.Worked examples
- 4.Practice
|
1. Review of prerequisite skills
- Review the definition of a ratio, ways representing ratios.
2. Develop working definitions of new terms
- Present two sets similar to the ones below to the class. Ask the
students to
provide more ordered pairs for each set. Define the terms means and extremes.
Ask the class to compute the product of the means and that of the extremes for
each pair. Get the class to list the attributes of Set A.
| Set A | Set B |
(1/2, 2/4), (3/4, 75/100)
(5:3, 20:12),
($8/h, $320/40h)
(dime/dozen, dollar/120) |
(1/2, 1/3), (1/10, 9/100)
(5:3, 12:20),
(100km/h, 180km/2h) |
- An equality of ratios, such as x/y = w/z is called a proportion.
- The proportionality may be written as x:y = w:z.
- Since x/y = w/z then there is a number k such that x/y = k and w/z = k.
- The constant K is called the constant of proportionality.
3. Worked Example 1:
The following table is a direct variation. Determine the constant of
proportionality.
|
| x |
y |
y/x |
|---|
| | 1 |
5 |
1/5 |
| |
2 |
10 |
2/10=1/5 |
The constant of proportionality 1/5.
Partially Worked Example 2:
- The key to successful problem solving is the ability to identify
the relating
variables. Provide the students with plenty of opportunity to practice. When
we use a gas barbecue, propane burns with oxygen to produce heat, carbon
dioxide and water vapour. For complete combustion of propane, one unit of
propane reacts with 5 units of oxygen to produce 3 units of carbon dioxide and
4 units of water vapour.
- a. How much oxygen is needed to burn 10 kg of propane?
- b. How much carbon dioxide is produced?
Solution:
- a. The amount of oxygen needed varies directly as the amount of
propane
present.
Let G = propane gas and P - propane gas.
G u P or G = kP
The oxygen to propane ratio is 5 to 1. We can set the proportion as 5:1 =
G:10kg
or
form the equation 5/1 = G/10kg. Solving for G, we find that 50 kg of oxygen is
needed.
(Ask the students to provide alternate methods, eg, table of values,
graphically)
- b. Assign part b, perhaps as group work.
4. Practice
- ... Holtmath 10, p. 180-181
- ... A. W. Math 10, p. 226-227
- ... Math Matters 10, p. 277-279
Chemistry problems involving masses and moles of molecules are excellent for
practice.
- Objective 21:
To solve proportions involving direct variation.
|
Systematic problem solving techniques should be emphasized. It is important
to identify the independent and dependent variables. Once the relating
variables are identified the problem may be solved as direct variation or as a
proportion. Some students may want to follow a flow chart such as the one
below:
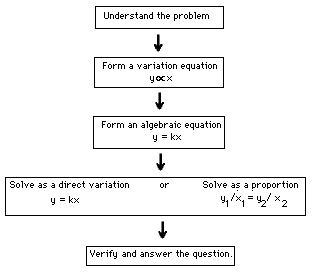
Practice questions are readily available in math and science texts. Ask each
student to concoct a number of problems for the class to solve. Make sure that
they are direct variations.
Objective 22:
-
To identify partial problems involving partial variation.
- Lesson Plan:
1. Review of prerequisite skills
- 2. Develop working definitions of new terms
- 3. Work out some examples
- 4. Practice
|
1. Review of prerequisite skills
- Mastery of direct variation is essential.
2. Develop working definitions of new terms
- Divide the chalkboard into halves with a vertical line.
- Sketch a number of graphs, placing graphs of partial variations on one side
and the rest on the other side.
- Student will quickly distinguish the two sets.
- Establish the fact:
- The graph of partial variation is a straight line and the starting point is
not the origin. The equation is of the form y = mx+b where b is not zero.
******************************
A question to ask:
In a direct variation, what is the effect on the second variable if the first
is doubled?
Is the effect the same in a partial variation?
******************************
Examples of partial variations:
- car rental charge = basic daily rate plus number of kilometres driven.
- salesman's income = basic monthly income plus percent of sales.
- speed of sound in air = 331m/s plus 0.59m/s for each degree Celsius above
zero.
- banquet cost = fixed hall rental plus number of plates of food served.
These are not partial variations:
- a teacher's monthly salary
- fuel consumption and speed
- the air pressure and altitude
- the volume of a gas and temperature
- the stopping distance of a car and the speed of the car
3. Worked example:
- A car salesman earns $500.00/month plus 2% of total sales. Construct a
table
of values, graph the variation.
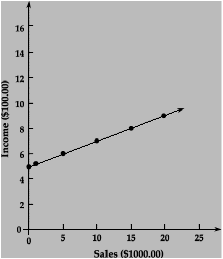
|
| Sales |
0 | 1000 | 5000 | 10 000 | 15 000 |
20 000 |
|---|
| Commission |
0 | 20 | 100 | 200 | 300 |
400 |
|---|
| Basic income |
500 | 500 | 500 | 500 | 500 |
500 |
|---|
| Total income |
500 | 520 | 600 | 700 | 800 |
900 |
|---|
| |
Extension:
- Compare the above with an alternate earning formula which offers no basic
monthly income but increases the commission rate from 2% to 3% of the sales.
4. Practice
- ... Holtmath, p. 183
- ... Math Matter 10, p. 281-283
- ... A. W. Math 10, p. 230-231 - Addison Wesley
- ... Questions from physics texts
- Objective 23:
- To solve problems involving partial variation.
|
- Treat partial variations as linear equations in slope-intercept
form, y = mx
+ b. Students need to be able to identify the independent variable, dependent
variable, the constant term (y- intercept) and to calculate the constant of
proportion (slope). Using a graphing calculator, the problem can easily be
solved.
- Convince the students to follow a problem solving strategy. One approach is
to follow a flow chart.
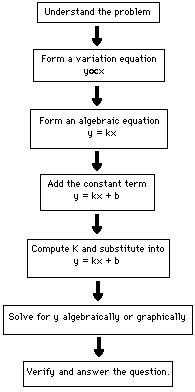
(SUGGESTION: Post the flow chart on the wall for a few days.)
- Worked example:
- Hockey jerseys are priced at $50.00 each plus $1.50 per letter. How
much will
Jerry Desjarlais' jersey cost if his last name is sewn on the back?
- Understand the problem:
- Given: $50.00/jersey and $1.50/letter
- Find: Cost of jersey with DESJARLAIS on it.
- Form a variation equation:
- Cost varies directly as number of letters
- C u L
- Form an algebraic equation:
- C = kL
- Add the constant term
- C = kL + 50
- Compute k and substitute:
- k = cost per letter
- k = $1.50
- C = 1.50L + 50
- Solve for y algebraically or graphically:
- Algebraically
- C = 1.50L + 50, L = number of letters in DESJARLAIS = 10
- By substitution we obtain C = 1.50*10 + 50 = 15 + 50 = 60
- Verify and answer the question:
Cost of letters = 10*1.50 = 15.00
Cost of jersey = 50.00
Total cost = 65.00
Practice questions
- ... Holtmath, p. 183
- ... Math Matter 10, p. 281-282
- ... A. W. Math 10, p. 230-231
- ... Questions from physics texts
Reprinted with permission from: This is a Yes: Concept Attainment. Saskatoon.
Saskatchewan Professional Development Unit and Saskatchewan Instruction
Development and Research Unit.
This unit comes from the The Stewart Resources Centre which provides
library resources and teacher-prepared materials for teachers in Saskatchewan.
To borrow materials or obtain a free catalogue listing unit and lesson
plans contact :
Stewart Resources Centre,
Sask. Teachers' Federation,
2317 Arlington Avenue,
Saskatoon, SK S7J 2H8;
phone 306-373-1660; fax 306-374-1122,
e-mail src@stf.sk.ca.
http://www.stf.sk.ca/
Go to Math Central
To return to the previous page use your browser's back button.






