A Trig Exercise Inspired by the Use of a Graphing Calculator.

Rick Seaman
Faculty of Education
University of Regina

This note is an example of a problem in algebra or trigonometry that is motivated by an exercise with a graphing calculator. The motivation was a question that came to Quandaries and Queries some time ago. The question was to find t if sin(t) - 2 cos(t) = 0, or equivantly, find the t-intercepts of the graph of f(t) = sin(t) - 2 cos(t). A student with a graphing calculator might plot the graph of this function for t between -360 degrees and 360 degrees and get the following.

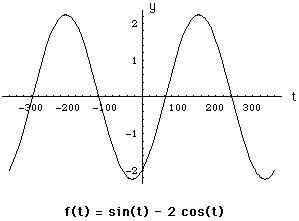
This graph resembles the graph of a sine function with an amplitude of approximately 2.2 and shifted approximately 60 degrees. The problem is then: Can you write the expression f(t) = sin(t) - 2 cos(t) so it is clear that this is an amplified and shifted sine function?

The necessary fact here is the trigonometric identity

sin(t-u) = sin(t) cos(u) - cos(t) sin(u) = cos(u) sin(t) - sin(u) cos(t).

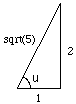
Compairing this to the expression for f(t) we see that sin(u) is twice as large as cos(u), so in the right triangle with angle u degrees and adjacent side 1 unit long the opposite side must be 2 units long and thus, by Pythagoras Theorem the hypotenuse is sqrt(5). Thus sin(u) = 2/sqrt(5) and cos(u) = 1/sqrt(5). Hence 

f(t) = sin(t) - 2 cos(t)
     = sqrt(5) (1/sqrt(5) sin(t) - 2/sqrt(5) cos(t))
     = sqrt(5) (cos(u) sin(t) - sin(u)  cos(t))
     = sqrt(5) sin(t - u)

where, from the second diagram, u = arctan(2). Using your calculator again sqrt(5) is approximately 2.24 and arctan(2) is approximately 63.4 degrees. So, as indicated by the calculator, sin(t) - 2 cos(t) can be written as a sine function with amplitude of approximately 2.24 and shifted approximately 63.4 degrees.

Problem: Can you write the expression f(t) = sin(t) - 2 cos(t) so it is clear that this is an amplified and shifted COSINE function?

Go to Math Central

To return to the previous page use your browser's back button.