On June 4, 1998, I took a trip to a welding shop northwest of Melfort. The name of the shop is "Holmspun Hoppers" and they make cone shaped hopper bottoms for grain bins. There are many mathematical processes involved in the making of the hoppers. My job was to find out exactly what these processes were.    The first job the welders did was cutting out the sheet metal and welding it together to form a circle. When the circle was laid out flat on the shop floor, a small wedge was cut out that had an angle of about 80 degrees. This angle varied depending on the size of the hopper that was ordered. Then a steel ring was placed around the circle to keep it from moving while a chain would pull up the middle of the circle. This would make the circle with the missing wedge into a cone shape.    Once the cone was hoisted up, it was welded together where the wedge once was. The ring was also welded to the bottom to keep it firm. When the cone was firmly welded, they attached 8 legs. They spaced them equally by calculating the circumference and dividing it by eight.    It was all quite interesting and the workers seemed to know a lot about Math. In the rest of my project I will show how to find the surface area and volume of the cone. I also included diagrams to give a clearer picture of my calculations. 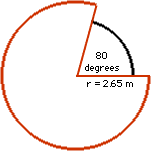Calculation # 1 Surface Area Laying Flat on the Shop Floor Since a wedge has been removed from the circle, the area of the circle will only be a percentage of the area of a complete circle. The wedge missing from the circle is 80 degrees. This means that 280 degrees of a full circular rotation is used. (360 - 80 = 280).    If the partial circle is 280 degrees then this represents 280 / 360 or 77% of a complete circle. Using the radius of the circle as 2.65 metres, I can now calculate the area of the partial circle. 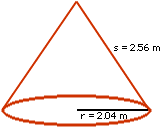The area will then be: (pi)(r)(r)(.77) = (3.14)(2.65)(2.65)(.77) = 16.98 square metres Calculation # 2 Surface Area When Raised into the Cone Shape Now that the flat circle has been drawn together into a 3 dimensional cone the radius of the cone is no longer the same as the radius of the flat circle in my previous calculation. The radius of the flat circle has now become what is called the slant height of the cone. The cone now has a radius of 2.04 metres and a slant height of 2.65 metres. Notice that the slant height is the same as the radius in the flat circle in calculation # 1. 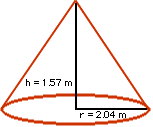The surface of the cone will then be: (pi)(r)(s) = (3.14)(2.04)(2.65) = 16.98 square metres Calculation # 3 The Volume of the Cone It is important to calculate the volume of the cone so that the farmer who orders the hopper will know how much grain will fit into it. I remembered from Math class that the volume of the cone is exactly one third the volume of the cylinder with the same circumference. The measurements I needed to take for this calculation were the true height of the cone and the radius of the cone. The true height was 1.57 metres and the radius was 2.04 metres. 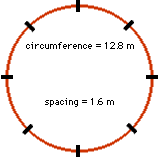The volume of the cone will be: (pi)(r)(r)(h)/3 = (3.14)(2.04)(2.04)(1.57)/3 = 6.84 cubic metres Calculation # 4 Spacing the Legs on the Hopper To put the eight legs on the hopper so that they are equally spaced we had to calculate the circumference of the hopper and then divide by 8. This was an easy calculation as I already had the radius measurement I needed. The spacing of the legs will be: (pi)(2r)/8 = (3.14)(2)(2.04)/8 = 1.60 metres (Editorial Note - A thank you is extended to Cal Strinholm, Adam Bourassa and Doug Arbogast of Holmspun Hoppers for their support of this educational project.) Return to Math Central To return to the previous page use your browser's back button.