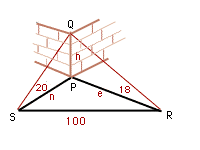
From a point S, the angle of elevation of the top of a tower due north of it is 20 degrees. From R, due east of the tower, the angle of elevation is 18 degrees. S and R are 100m apart. Show that the height of the tower is given by
![]()
|
My name is Calvin and I have a year 12 question for you to help me with.
From a point S, the angle of elevation of the top of a tower due north of it is 20 degrees. From R, due east of the tower, the angle of elevation is 18 degrees. S and R are 100m apart. Show that the height of the tower is given by
|
|
From the diagram h/e = tan 18, h/n=tan 20 and e^2 + n^2 = 100^2. Thus 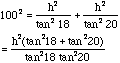 . . Thus |
|
![]() =
= 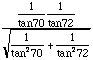 =
= 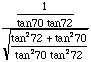 =
= 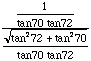 =
= ![]()
Another way to present the proof this identity is to perform mathematical operations on the two expressions separately and see if they can be reduced to identical expressions. This is the "two column" presentation you often see in proofs of trigonometric identities. I quite often use an equal sign or identity symbol with a question mark above to indicate a questionable equality. Below is such a sequence of algebraic manipulations.
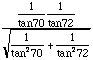 |
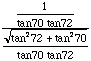 |
|
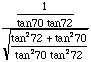 |
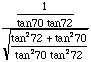 |
Since the last two expressions are identical we have shown that
![]() .
.
Because of this "two column" presentation it is necessary to remind students that they can only perform operations on one column at a time. Calvin's question is an example of a place where proving a trig identity is necessary and illustrates the operational constraint placed on the "two column" presentation.
To return to the previous page use your browser's back button.