When looking at probabilities we consider the ratio of the number of favourable outcomes to the total number of outcomes; graphically, if the large rectangle represents our sample space S,
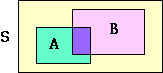
then (if |T| denotes size of a set T)the probability of the event A is
P(A) = |A| / |S|.
In discussing conditional probabilities we use the notation P(A|B) to denote the probability of the event A happening given that we know event B has occurred already. This restricts the sample space under consideration to the set B so that P(A|B) is the ratio of the number of outcomes in 
to the number of outcomes in B, i.e.
P(A|B) = |A 
B| / |B|
now this may be rewritten as P(A|B) = (|A
B| / |S|) / (|B| / |S|), equivalently
P(A|B) = P(A
B) / P(B)
or
P(A
B) = P(A|B) P(B).
A typical use of conditional probabilities is in the testing for disease. Tests for disease are not 100% accurate and we need to be aware that a positive test result may not in fact mean that the disease is present, thus requiring invasive or expensive procedures. Such a result is called a false positive. Of course it is desirable to minimize false positives which we do by retesting or by using alternate tests.
The following example is interesting in that when asked of a group of 60 students and staff at the Harvard Medical School, only 11 answered correctly.
We know that the prevalence of a particular disease is 1/1000 in the general population. A test for this ailment has a false positive rate of 5%, that is, 5% of the time the test will erroneously indicate that the disease is present when in fact it is not. We are also told that 98% of the people with the disease will in fact test positive. Assuming that you know nothing about particular individuals or their symptoms, what is the probability that a person that has tested positive does in fact have the disease?
What's the problem here? Why do so many people not even estimate the answer very well? Why do they often guess more than a 50% chance? Why is it that most people would be immediately worried unecessarilly? The problem lies in the relatively small probability of any one having the disease.
First let's model this: we will use D to denote presence of the disease, D to denote it is not present, we will use + for positive tests and -for negative tests. Our problem then translates as
Given that P(D) = 
, P(+|D) = 
, and that P(+|D) = 
, find P(D|+).
A convenient way to present this is with a tree diagram
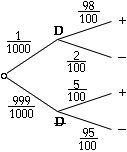
From these branches we see that
P(D
+) = 
and
P(+) = P(D
+) + P(D
+) = 
Thus P(D|+) = P(D
+) / P(+) = (98 /100000) / (5093/100000) = .01924…
that is a little less than 2% chance that the individual has the disease! Graphically the picture is something like
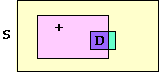
and the crucial point is that D is only 1/1000 of S!
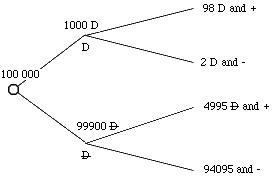
It may be instructive to think of the population S having size 100000 (see below), then only 100 would be expected to have the disease. If you tested the whole population, all 100000 of them, then the test would accurately pick up 98 diseased people but the 5% false positives amount to 4995 people. That is, only 98 of the total 5093 people showing positive are indeed ailing with the disease.
To return to the previous page use your browser's back button.