THE BINOMIAL THEOREM AND THE PRINCIPLE OF INCLUSION & EXCLUSION - P.I.E.
D. Hanson
Suppose we are told that in a collection of 100 students, 50 take Algebra, 23 take Trigonometry, and 17 take both Algebra and Trigonometry. How many students take at least one of these courses?
This is a standard counting problem that we often use Venn diagrams to model and solve. If the sets of students in Algebra and Trig are denoted by A1 and A2 we have |A1| = 50, |A2| = 23 and |A1 ![]() A2| = 17. We evaluate |A1
A2| = 17. We evaluate |A1![]() A2| as
A2| as
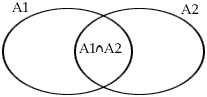
The idea here is that we count (include) all the elements and then subtract (exclude) those we have counted twice, those in A1 ![]() A2. If we use Sk to denote the sum of all possible choices of intersections of sets taken k at a time we can abbreviate this as
A2. If we use Sk to denote the sum of all possible choices of intersections of sets taken k at a time we can abbreviate this as
Suppose instead that we have 50 take Algebra, 23 take Trig, 42 take English, 17 take both Algebra and Trig, 13 take Trig and English, 31 take Algebra and English, and 8 take all three courses. How many students take at least one of these courses? Thus, if the sets of students are denoted by A1, A2 and A3, we have
|A1
and |A1
| |A1 |
= | (| A1| + |A2| + |A3|) - (|A1 |A1 |
| = | (50 + 23 + 42) - (17 + 13 + 31) + 8 = 115 - 61 + 8 | |
| = | 62. |
We abbreviate this as
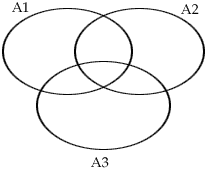
The idea here is to count (include) all elements that appear in each of the sets (those in A1, A2 and A3), but having done that note that we have now counted some of them twice (those belonging to two sets namely those in A1![]() A2, in A1
A2, in A1![]() A3 and in A2
A3 and in A2 ![]() A3), so they must be excluded (subtracted), and finally, having subtracted all of these, at this point some have now not been included at all, (those in A1
A3), so they must be excluded (subtracted), and finally, having subtracted all of these, at this point some have now not been included at all, (those in A1 ![]() A2
A2 ![]() A3) and they must be added (included) back in.
A3) and they must be added (included) back in.
Now what if for example there were five or six sets, or in general n sets, rather than three sets? Letís suppose that we have n sets A1, A2, ... An and we want to evaluate
|A1 ![]() A2
A2 ![]() ...
...![]() An|. Again we use Sk to denote the sum of all possible choices of intersections of sets taken k at a time and we claim
An|. Again we use Sk to denote the sum of all possible choices of intersections of sets taken k at a time and we claim
The Principle of Inclusion and Exclusion - P.I.E.
Let's abbreviate | A1![]() A2
A2 ![]() ...
...![]() An| by N, then we have to show that
An| by N, then we have to show that
N - S1 + S2 - S3+ S4 - S5 + - ... + (-1)nSn = 0.
Recall that the Binomial Theorem states that
and in particular this tells us, letting x = 1 and y = -1, that
The element z will be counted once = ![]() times by N; z will be counted p =
times by N; z will be counted p = ![]() times by S1 - since it is in p different sets; z will be counted
times by S1 - since it is in p different sets; z will be counted ![]() times by S2 - since it is in that many pairs of sets; z will be counted
times by S2 - since it is in that many pairs of sets; z will be counted ![]() times by S3 - since it is in that many triples of sets; ...; z will be counted
times by S3 - since it is in that many triples of sets; ...; z will be counted ![]() times by Sk - since it is in that many choices of k of the p sets; ...; finally z will be counted once =
times by Sk - since it is in that many choices of k of the p sets; ...; finally z will be counted once = ![]() times by Sp as it is in p sets. All told z is counted
times by Sp as it is in p sets. All told z is counted
times as required.
The P.I.E. has many applications in mathematics at a sophisticated level, for example to count the number of onto functions from a set of size n to a set of size m - why would you want to know that? Well it maybe that your running a government agency and you have 7 contracts to hand out to 4 companies and each must get at least one. How many ways can that be done? Using the P.I.E. we can show that there are ![]() ways to do this.
ways to do this.
Before we close let us illustrate the P.I.E. in action with a simple number theory problem:
How many integers from the set {1, 2, ..., 1000} are not divisible by any of the primes 2, 3, 5, and 7? To solve this we look at the complementary problem of how many of these integers are divisible by 2, 3, 5, or 7? For notational convenience let us denote by A2, A3, A5 and A7 the sets of integers under discussion that are divisible by 2, 3, 5 and 7 respectively. Since every second integer is a multiple of 2, every third a multiple of 3, etc., we see that
and S1 = 500 + 333 + 200 + 142 = 1175;
|A2
|A3
and S2 = 166 + 100 + 71 + 66 + 47 + 28 = 478;
|A2
|A2
and S3 = 33 + 23 + 14 + 9 = 79;
and |A2
Thus | A2 ![]() A3
A3 ![]() A5
A5 ![]() A7| = S1 - S2 + S3- S4 = 1175 - 478 + 79 - 4 = 772 and the original problem of how many integers from the set {1, 2, ..., 1000} are not divisible by any of the primes 2, 3, 5, and 7 has the solution of 1000 - 772 = 228.
A7| = S1 - S2 + S3- S4 = 1175 - 478 + 79 - 4 = 772 and the original problem of how many integers from the set {1, 2, ..., 1000} are not divisible by any of the primes 2, 3, 5, and 7 has the solution of 1000 - 772 = 228.