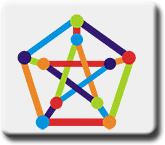The basic structure of our logo is what is known as a graph.

A graph has a set of vertices (points), some pairs of which are joined by an edge (line). The particular graph we are using is known as the Petersen graph after the 19th century Danish mathematician, Julius Petersen.

Assigning colours to the vertices of a graph in such a way that no two vertices that are joined by an edge have the same colour is known as a proper colouring of the vertices. Assigning colours to the edges of a graph in such a way that no two edges that meet at a vertex have the same colour is known as a proper colouring of the edges. A total colouring of a graph is one in which not only do we have a proper colouring of both the vertices and edges but also we have that no vertex and edge of the same colour are incident.

Our logo is totally coloured in five colours; you might try to see if four colours is sufficient. In general it is an unsolved problem as to how few colours we must use to totally colour a graph. If the degree of a vertex is the number of edges incident with it, then it is easy to see that we need at least the size of the largest degree + 1 colours for a total colouring. It is conjectured that we can always get by with at most the the size of the largest degree + 2 colours.

Graph colouring problems in general deal with the fundamental problem of partitioning sets of objects into classes according to certain rules. These problems have applications in such areas as time tabling and scheduling.