Natasha Glydon

Benjamin Franklin is famous for his money making and money saving trends, among various inventions.  He is noted to have said, “A penny saved is a penny earned.”  It is not surprising then that when Franklin died in 1790, he left a plan that would enrich the cities of Boston and Philadelphia.   This plan was based on a mathematical concept known as exponential growth.  Exponential growth is the term used to describe compound interest, which is what Franklin thought would make Boston and Philadelphia very wealthy cities in a couple hundred years.

Image reproduced with permission of Daniel Paul

In his will, Benjamin Franklin left his money and assets to various family members and friends.  Interestingly, he also left 1000 pounds (just under 5000 Canadian dollars) each to Boston and Philadelphia.  There were some restrictions, however.  Both cities were to invest the money, at an interest rate of 5% (compounded yearly) and leave it untouched for 100 years.  At the end of the 100 years, the city was allowed to spend three quarters of it on a city improvement project and the rest was to be reinvested for another 100 hundred years at the same interest rate.

Franklin estimated his donation as follows:
1000 pounds is about $5000 Canadian dollars.  By using a formula for compound interest, we can estimate an answer as to the total amount of Franklin’s donation to the cities. The formula for compound interest is:

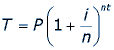
Where T is the total amount in the fund, including the interest accumulated over t years, compounded n times annually, at an interest rate of i on a principle investment of P dollars.  Let’s substitute some values we know.

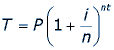
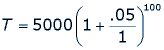
This will give us the total amount of the fund, including the interest, accumulated over 100 years.

T = $657, 506

So, in just 100 years, Franklin’s initial investment would increase by more than $650,000!  This is because of compound interest.  Now, Franklin’s restrictions on the money stated that the city could spend three quarters of the money and then re-invest the rest. 

Well, three quarters of $657,506 is $493,130.  That leaves $164,376 to be re-invested under the same conditions.  Now, our principle rate, P, is $164,376.

T = $21,615,651

So, at the end of the 200 years, each city should have over 21 million dollars in their investment fund.

Unfortunately, because of tough times during those two hundred years, it was difficult for Boston and Philadelphia to get a good 5% interest rate each year.  As a result, after 200 years, the Boston fund only had $5,533,316 and Philadelphia was only able to collect $2,497,933 in their fund.

Compound interest works on the basis of exponents.  In fact, the exponent is the money making difference between compound interest and simple interest.  Compound interest allows you to make money on the interest you previously earned from your principle amount.  It is important for people to understand how exponents work so that they are able to make the most money from their investments.

Compounded yearly means that compound interest is calculated once a year.  If Franklin’s money had earned interest by being compounded monthly, how much would the fund be worth after the first 100 years?

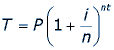
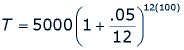
T = $734,397

Notice that this is more than the $657,506 that accumulated over 100 years with interest being compounded only once a year.

In the same way, banks make money.  When you receive a loan from the bank or use a credit card, the bank or credit card company charges you interest.  This interest rate is often much higher than what is offered for a savings account, usually 10-20%, and, the longer you take to repay your loan, the more interest you have to pay.  Compound interest or exponential growth is also used when you mortgage a house or make car payments.

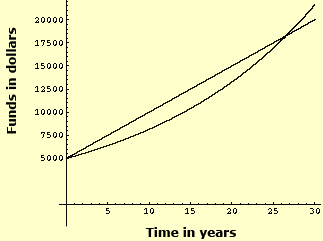
The above graph shows the exponential growth of Franklin's money (the curved line). The straight line represents a linear growth of $500 per year. In less than thirty years, the exponential growth surpasses the linear. Imagine how great of a difference there will be after 100 or 200 years. Exponential growth is very rapid and sizeable. The graph below shows just how great the difference is after only 100 years.

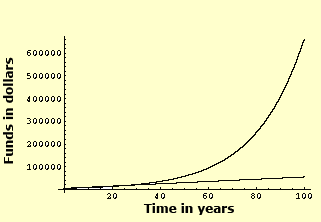
The graph of an exponential function describes occurrences in nature, such as the growing deer population, for example.  However, hunting controls the deer population so that there is enough food for all the deer.  The human population also grows exponentially.  Researchers study this information to predict future population numbers.