Natasha Glydon
Math is in every kitchen, on every recipe card, and at each holiday gathering. The mathematics of cooking often goes unnoticed, but in reality, there is a large quantity of math skills involved in cooking and baking.
Conversions
Most ranges have dials that display the cooking temperature of the oven. In North America, most of these temperatures are written in Fahrenheit and usually are in increments of 25°. In Canada, recipe and oven temperatures are often presented in degrees Celsius. It is important then to understand how to convert a Fahrenheit temperature to an appropriate Celsius temperature. For example, let’s say your oven displays Fahrenheit temperatures with 50° increments. Your recipe tells you to bake your dish at 220°C. What temperature do you turn your oven to? Well, you will need to convert 220°C to a Fahrenheit measurement.
We use this formula to convert Celsius to Fahrenheit:
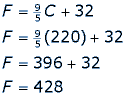
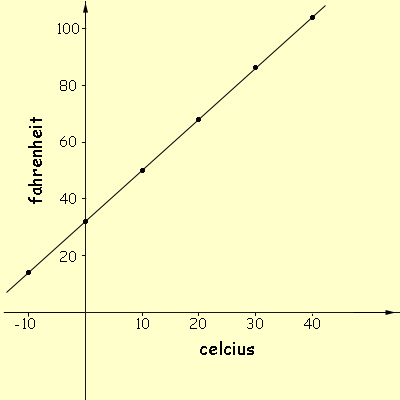
To make sure you do not over bake the cookies, you will need to set the oven to 428°F. But remember, your oven only displays the temperature in 50° increments, so you must estimate on the dial where 428°F is, somewhere between 400°F and 450°F. The relationship between celsius and fahrenheit is a linear function:
![]()
We also use conversions when we bake or cook to convert sizes and amounts. Many recipes are written in imperial units (teaspoon, tablespoons, and cups). Some newer recipes and measuring devices in Canada are labeled in metric units, such as milliliters (mL). If the recipe calls for ½ cup of butter and your measuring equipment is labeled in mL, how will you know which measurement to use? We can apply this conversion formula: 1 cup = 237mL. This means that ½ cup = 118.5mL. Again, this exact measurement is probably not on the measuring cup. It is probably closest to 125mL, so we will again have to estimate.
Making Enough
Most recipes give guidelines as to how much a single batch will produce. But what if you want more? It seems too time consuming to mix up another batch. What if the recipe makes only one dozen cupcakes and you need three dozen? Clearly, three dozen is three times more than 1 dozen, so we can multiply all the ingredients by three to make a larger batch. It is also important to understand how to multiply fractions. If the cupcake recipe calls for ¾ cup of milk and we want to triple it, we need to know that:
![]()
So, we will need 2 and 1/4 cups of milk to make three dozen cupcakes.
This knowledge of fractions is also helpful when we need to make our batch smaller. For example, recipe guidelines approximate that each batch will yield 6 dozen cookies. But, my family is small and I only want 2 dozen cookies. First, we need to see the relationship between 2 and 6. We can see that 2 dozen is one third (1/3) of 6 dozen because 2 x 3 = 6. That means that in order to make only 2 dozen cookies, we will need to use one third of each ingredient. So, if the recipe asks for 2 teaspoons of baking powder, we will only need 2/3 of a teaspoon, since
![]()
If we do not have a measuring spoon that is equal to 2/3 teaspoon, we may need to use 1/3 twice, or estimate using ¼.
When recipes indicate how much a particular batch will make, they give a general amount of food. If we are cooking for a group, we need to estimate how much each person will eat and make appropriate amounts of the particular item. For example, if a package of spaghetti makes 1L of cooked spaghetti, will we have enough to feed six people with one package? If not, how much of a second package will we have to use? First, we need to estimate how much each person will eat. We can guess that each person will eat 1 cup of spaghetti, which is 237mL. For convenience sake, we can round this to 250mL. That means that six people will eat 1500mL of spaghetti. If 1L=1000mL, we know that we will need to make one whole package, plus half of the second package to ensure that everyone has enough to eat.
Being Creative
Sometimes, we may not have all the ingredients to make a recipe, but we may have something we can fittingly substitute. How does this affect the measurement amounts in the recipe? For example, let’s imagine we are making Rice Krispie cake. The recipe calls for 32 large marshmallows, but we only have miniature marshmallows. We can still use the small marshmallows, but we will need to estimate how many mini marshmallows would make one large marshmallow, and multiply that number by 32.
What if you want to spice up your chocolate chip cookies by adding almonds and coconut? Your recipe calls for 2 cups of chocolate chips, but you want to add 1/3 cup of almonds and 1/6 cup of coconut. How much chocolate chips do you still have to add? Well, we simply need to subtract, using fractions.
![]()
We still need to add 1 and ½ cups of chocolate chips. It is important to remember that when adding and subtracting fractions, we need to use a common denominator.
Weight
Weight often affects cooking time. Consider the following hypothetical situation: we are cooking an 8 pound turkey for Christmas dinner. If the turkey needs to thaw in the refrigerator for 24 hours, per 5 pounds, we need to take the turkey out of the freezer in advance. We can use a proportional relation to help us decide how early to thaw the turkey.
 |
The above proportion reads as follows: 5 pounds is to 24 hours as 8 pounds is to x hours. By cross-multiplying and dividing, we can find an answer of 38.4 hours, which is the solution for x.
If we are instructed to cook the turkey for 20 minutes per pound, how long do we need to cook the turkey? Well, 20 minutes per pound for 8 pounds is 20 x 8 = 160 minutes. And, 160 minutes is two hours and 40 minutes. If we only knew the weight of our turkey in kilograms, we would need another conversion formula (kilograms to pounds) to find the weight of the turkey in pounds first, and then apply the recommendations.
Cost
We also use math when cooking and baking to estimate the cost of a certain dish. We can understand that cheesecake is more expensive to make than a batch of cookies, particularly when people buy ingredients such as flour, sugar, and butter in bulk and cream cheese is more expensive. When comparing recipes, it may be beneficial to estimate the cost of each recipe.
Mathematical skills are used quite frequently when baking and cooking. It can be very helpful to understand how math affects the quality of culinary in order to make the most delicious meals and treats.
Try this cooking Web Quest that involves math.
