Natasha Glydon
Exponential decay is a particular form of a very rapid decrease in some quantity. One specific example of exponential decay is purified kerosene, used for jet fuel. The kerosene is purified by removing pollutants, using a clay filter. Suppose the clay is in a pipe and as the kerosene flows through the pipe, every foot of clay removes 20% of the pollutants, leaving 80%. If Po is the initial amount of pollutants in the kerosene, then the amount left, P, after n feet of pipe can be represented by the following equation:
![]()
Suppose that the pollutants must be reduced to 10% in order for the kerosene to be used for jet fuel. How long does the pipe have to be to ensure that there is only 10% of the pollutants left in the kerosene?
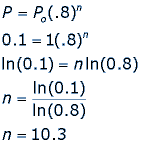
This means that we need a pipe that is 10.3 feet long in order for the pollutants to be reduced to 10% of their starting amount.
Carbon 14 Dating
Archaeologists use the exponential, radioactive decay of carbon 14 to estimate the death dates of organic material. The stable form of carbon is carbon 12 and the radioactive isotope carbon 14 decays over time into nitrogen 14 and other particles. Carbon is naturally in all living organisms and is replenished in the tissues by eating other organisms or by breathing air that contains carbon. At any particular time all living organisms have approximately the same ratio of carbon 12 to carbon 14 in their tissues. When an organism dies it ceases to replenish carbon in its tissues and the decay of carbon 14 to nitrogen 14 changes the ratio of carbon 12 to carbon 14. Experts can compare the ratio of carbon 12 to carbon 14 in dead material to the ratio when the organism was alive to estimate the date of its death. Radiocarbon dating can be used on samples of bone, cloth, wood and plant fibers.The half-life of a radioactive isotope describes the amount of time that it takes half of the isotope in a sample to decay. In the case of radiocarbon dating, the half-life of carbon 14 is 5,730 years. This half life is a relatively small number, which means that carbon 14 dating is not particularly helpful for very recent deaths and deaths more than 50,000 years ago. After 5,730 years, the amount of carbon 14 left in the body is half of the original amount. If the amount of carbon 14 is halved every 5,730 years, it will not take very long to reach an amount that is too small to analyze. When finding the age of an organic organism we need to consider the half-life of carbon 14 as well as the rate of decay, which is –0.693.
For example, say a fossil is found that has 35% carbon 14 compared to the living sample. How old is the fossil?
We can use a formula for carbon 14 dating to find the answer.
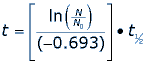
Where t1/2 is the half-life of the isotope carbon 14, t is the age of the fossil (or the date of death) and ln() is the natural logarithm function. If the fossil has 35% of its carbon 14 still, then we can substitute values into our equation.
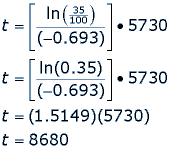
So, the fossil is 8,680 years old, meaning the living organism died 8,680 years ago.
Plutonium
Plutonium 239 is a man-made radioactive isotope. Plutonium 239 is used to make nuclear explosives. Plutonium 239 has a half-life of 24,110 years, which means that it would take 240,000 years to decay to a safe amount. Plutonium 239 decays exponentially into lead, but it causes concerns for humans because the tiny particles of plutonium react with oxygen and water and can be extremely flammable. Since the half-life of Plutonium 239 is so high (even in comparison to the carbon 14 half-life of 5,730 years) humans must be very cautious of the way they dispose of plutonium. Scientists are looking for safe ways for disposing plutonium.
Exponential Decay in Your Daily Life
We can see exponential decay in other areas as well. Let’s say that I can make a dozen cookies in 2 hours. I am just learning the recipe so it takes me more time to look back and forth and double check. The more cookies I make, the more practice I have and the less time it takes me to bake the cookies. This can be represented as an exponential function if we say that every time I bake cookies my time decreases by 1/5 of the previous time.
We can use exponential decay to represent a number of different things. Most importantly, exponential decay is not linear and the decrease is rapid at first, but not constant. It is often used to describe population decreases (or increases, which depicts exponential growth) and can be seen using a graph of an exponential curve.
