Some games are considered more risky than others based on their probabilities of winning and their expected value.  The expected value is what the player can expect to win or lose if they were to play many times with the same bet.  For example, when playing Roulette, let’s say that a player bets $10 on red, with a payout of 1:1.  The expected value of that bet played over and over can be expressed as follows.

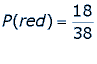The winning amount for one bet is $10

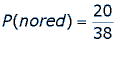The losing amount for one bet is -$10

Expected value is calculated as follows:

[(probability of winning)(amount won per bet) - (probability of losing)(amount lost per bet)]

We can represent this mathematically using the values from above:

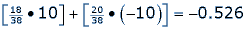
This means that if a player were to make this same bet of $10 on red over and over again, the player can expect to lose $0.53 for each bet of $10.  A player has better chances of winning money with a positive expected value.

Image reproduced with permission of Retirement Roulette