Similar to the Loran system, GPS works successfully with the transmission of signals, traveling at the speed of light.  In the case of GPS, we are working with satellites instead of stations.GPD uses twenty-four satellites that orbit the entire earth, and hence it can provide important navigational information anywhere in the world.  

Also similar to the Loran, three satellites are needed to find the altitude, longitude, and latitude of a GPS receiver on earth.  The satellites send signals that are picked up by the GPS receivers, just like the Loran system.  The receiver is then able to find the distance from each of the three satellites to the receiver. Because we know how fast the signals are traveling (the speed of light), the simple distance formula provides us with this information (distance = speed x time ).  Instead of using the hyperbola, each of the three satellites becomes the centre for a sphere; with a radius equal to the distance we calculated using the formula.  The three spheres will intersect at two points, one of which is usually unrealistic, perhaps below sea level.  If there are two plausible points, a fourth satellite distance calculation may be needed.  The appropriate point of intersection is the location of the receiver.  The process of using three (or more) spheres to locate a point is called trilateration.

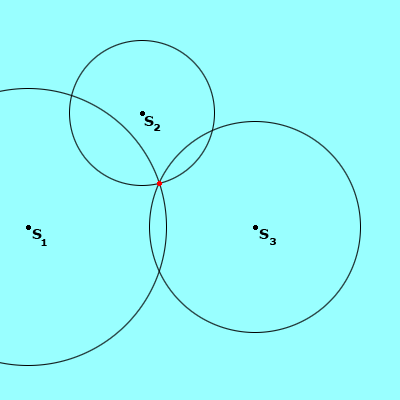
The picture above shows three circles of varying distances, centered around satellites (S₁ , S₂ , and S₃ ). The point where the three circles (or spheres, as is the case with GPS) meet is the location of the GPS receiver.