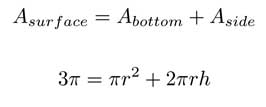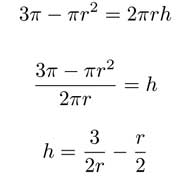Finding an optimal value of a function in the most simple cases usually means finding a maximum or minimum value. For example, consider a container in the shape of a right circular cylinder with no top has surface area 3 π m². What height h and base radius r will maximize the volume of the cylinder?

Let r be the radius of the circular base and h be the height of the cylinder. Both r & h are in metres.

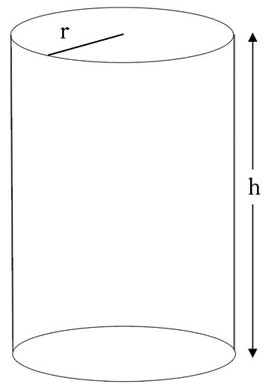The total surface area of the cylinder with an open top is so that height can be written as

We want to maximize the total volume of the cylinder

but before we differentiate, we can reduce the number of variables by substituting in our expression for h in terms of r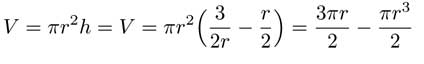
Now differentiate this equation, we get

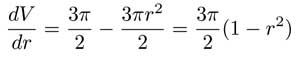
Looking at the graph of radius versus volume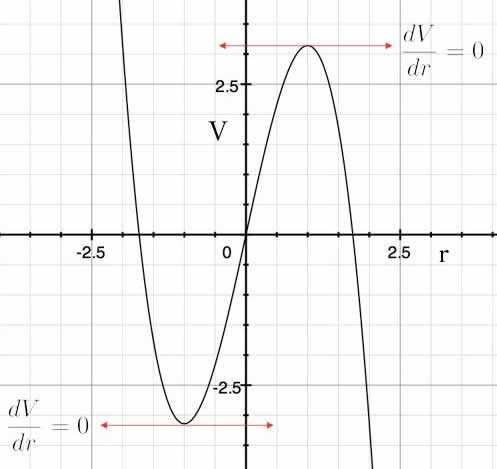

we can see that the maximum and minimum occur when

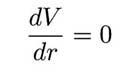
so then

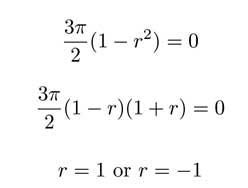
Since variable r measures a distance then r > 0 so the only possible value is . Using our known radius, it follows that and then the maximum volume is .

More generally, optimization problems means finding the best possible solution that fits all the necessary criteria. Equations needed in solving for optimizing the radius of a pipe that cools concrete like


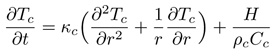
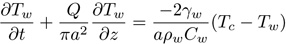
are difficult and time consuming to solve without the use of a computer with programs like MATLAB, Maple or Mathematica . [Warning: external links open in a new window]

Cooling a Concrete Slab - Main Page

IPSW Main Page