First radius r needs to be determined to optimize the system. To begin, the simplest case must be considered: the heat exchange between a single pipe of radius a carrying water with a 'sleeve' of concrete of radius r surrounding it. The concrete sleeve can be considered to be the volume of concrete the water pipe can cool effectively. The diameter (2r) can thought to be the spacing between pipes in the network. 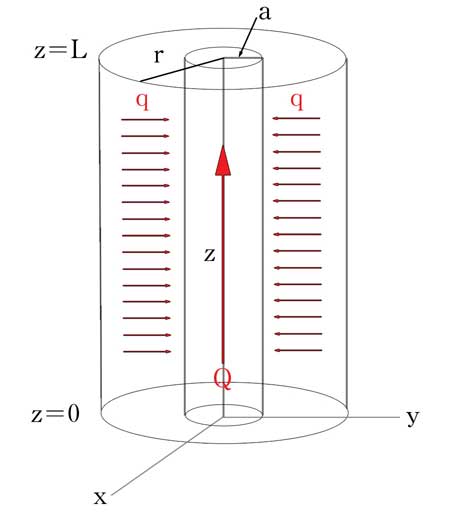
The problem breaks up into two connected parts: heat transfered radially from the concrete sleeve to the water and heat transported along the pipe by the water.
Heat diffusion within the Concrete Cylinder

| - temperature of the concrete | |
| - change in temperature of the concrete over time | |
| - heat flow from concrete to water | |
| - thermal diffusion coefficient for concrete | |
 |
- rate heat is transfered radially |
| - temperature increase due to mineral hydration | |
| - heat production per volume due to hydration; function of time | |
| - density of concrete | |
| - specific heat of concrete |
Heat Transfer Along the Pipe
![]()
| - temperature of the water | |
| - change in temperature of the water over time | |
| - the volume flux of water through the pipe, assumed constant | |
| - change in temperature of the water over a distance travelled | |
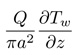 |
- change in temperature of water over a distance depends on how fast the water is flowing through the pipe |
| - radius of the pipe | |
| - heat transfer coefficient for the flow through the pipe | |
| - density of water | |
| - specific heat of water | |
| - volumetric heat capacity of water; ability of a volume of water to store energy while undergoing a temperature change | |
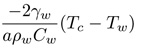 |
- rate of heat exchange of the water and concrete depends on the heat capacity of the water and the temperature difference. |
After some manipulations of the two governing equations, the radius can be optimized using numerical analysis.
