A linear program was written to minimize "x" such that Ax ≥ b and x ≥ 0:

(In order to understand the above formulation and the explanation below, you'll need to know some terminology.)
In the formulation of the linear program, A is a binary protein/drug matrix. This means that the columns represent the drugs and the rows represent the proteins that could be targeted.
Also, "x" is what we’re looking for. It is a vector and each entry in this vector represents the proportion of each of the drugs that should be given. "b" is another vector, and it represents what is being targeted. Each entry of this vector represents a unique protein. This vector is binary, meaning that a 1 represents the targets that are being treated and a 0 represents the targets that do not need to be treated.
Overall, Ax (the protein/drug matrix multiplied by the solution vector "x") is the real dosage that should be given to the patient. And Ax ≥ b because the real dosage being given to the patient needs to be more than the target amount.
Example:
Using the example of Basal Cell Carcinoma (the most common form of cancer & most common form of skin cancer), there are 14 targets that could be treated and 18 approved drugs that could treat these targets (from Drug Bank)
Using this information, a 14×18 matrix "A" is formed. This matrix is below
In the example, retinoic acid receptor gamma-2 is targeted (which is row 9 of the matrix A). This target is simply an example, there was not enough information to know what would be targeted in a real application of this solution.
Using MATLAB to solve the linear program, it was obtained that
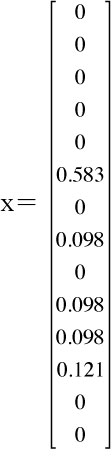 |
This is the proportion of each drug to give the patient in order to most effectively block retinoic receptor gamma-2 in the patient’s system. It would be best to also include drug interactions in this model. By including these interactions, we ensure that patients are not being given drugs that react adversely to one another and would cause other problems. To do this, our linear program was changed to a mixed-integer program by introducing two new variables; under the assumption that drug 1 interacts badly with drug 2, we let i1 stand for drug 1 and i2 stand for drug 2. In order to ensure that both drugs are not used together, it is written into the program that i1 and i2 have to be either 1's or 0's and that i1 + i2 ≤ 1. Therefore, either both drugs are 0 (meaning neither one of them are being used), or strictly one of them is 1, meaning that only one of them is being used – never both. |
It was also considered that a physician may be able to simply deduct that one of the interacting drugs would be better for their patient than the other. In this case, the physician could simply remove the drug they don't want from the overall system by removing its column in matrix A. This method would also be used in the case that the patient has an allergy to a certain drug that is in the matrix A.
