Graphs are abstract structures used to model relationships between two or more objects. These graphs are not the same as the graphs of functions that are commonly studied in secondary school; instead, these graphs have vertices that are connected by edges and these edges represent relationships between the vertices.
Visually, the vertices appear as dots and the edges appear as lines connecting these dots. It is important to remember that the orientation of the edges and vertices is not important in graph theory; the study of graphs involves the number of edges connecting each vertex. For example, the two graphs below are identical in graph theory:

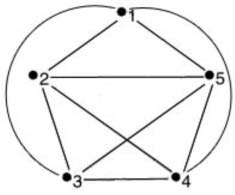
These are the same because there are the same numbers of edges extending from each vertex. The direction of the edges does not matter. In general, graph theory is the mathematical and scientific study of these graphs.
There are several different types of graphs, and some of these types are outlined below. The type of graph is listed, followed by a description of the properties of that type of graph and the number of searchers that are needed to search it (just for the purposes of this problem). Lastly, a visual representation of that type of graph is provided.
Path graphs ("p" graphs)
- Have only one edge connecting each pair of vertices.
- Paths can be searched with one person.
| P3 graph - path ("p") graph with 3 vertices. |
Circular/cycle graphs ("c" graphs)
- Creates a loop where each vertex has two edges that connect to it.
- Circular/cycle graphs can be searched with two people; either the searchers can move in opposite directions or one can stay stationary and the other can search the rest of the graph.
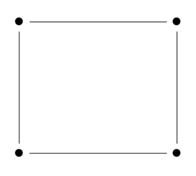 |
C4 graph - circular ("c") graph with 4 vertices. |
Star graphs
- Edges radiate out from a central vertex.
- Star graphs can be searched with two people; one searcher can stand in the center and the other can search each path.
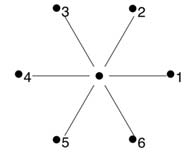 |
| Star graph with 7 vertices |
Complete graphs ("k" graphs)
- Every vertex connects to every other vertex through edges.
- Complete graphs can be searched with the same number of people as there are vertices. This means that since the graph below has 5 vertices (intersections), it can be searched with 5 searchers.
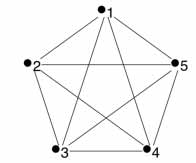 |
| K5 graph - complete ("k") graph with 5 vertices. |
