Since a cave is simply a large set of pathways and intersections, it can be modeled as a graph with the pathways being represented as edges and the intersections represented by vertices.
Below is an example of modeling a piece of the Regina map as a graph. Intersections become vertices and roads become edges.
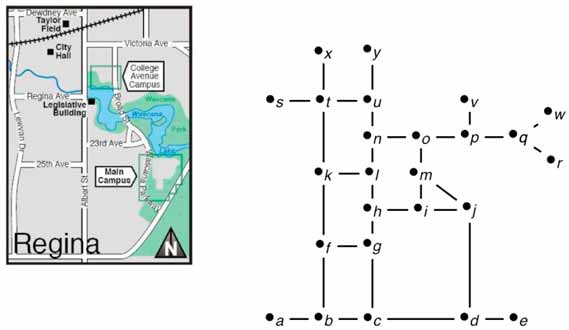
By breaking this graph down into small pieces (i.e., sub-graphs) it becomes obvious that there are several different types of graphs in the whole – there are paths, cycles and even parts where there is complete graphs – and each of these are linked together, creating our map.
Typically, there are two different ways to search graphs – either by searching just the vertices, or by searching each of the edges. In this study, the focus is on searching the edges of the graphs. This means that the searchers will move along the different corridors making sure that the lost spelunker is not anywhere in that corridor.
Something else to consider is that the lost spelunker may be wandering around inside the caves while they are lost and not just standing in a stationary position. This means that the searchers have to make sure that the lost spelunker cannot unknowingly circle back behind them, into a corridor they have already searched. This also means that the searchers occasionally have to leave people at vertices in a stationary spot, so that if the lost spelunker is wandering around, the stationary searcher will be able to find them.
One-tick searching
One-tick searching means that each searcher is allowed to move at most once. Searchers can begin at any vertex (there is no set "entrance"). Some vertices will have searchers who will stay stationary at one vertex and these searchers are referred to as "blockers". In the case of the 4th order circular graph (C4, a circular graph with 4 vertices), you would need 4 searchers to search it, but you wouldn't need any blockers. This example is shown below.
In this example the numbers indicate the searchers; an edge labeled with the number 1 indicates that searcher number 1 moves along that edge and a number 2 indicates that searcher number 2 moves along that edge, etc.
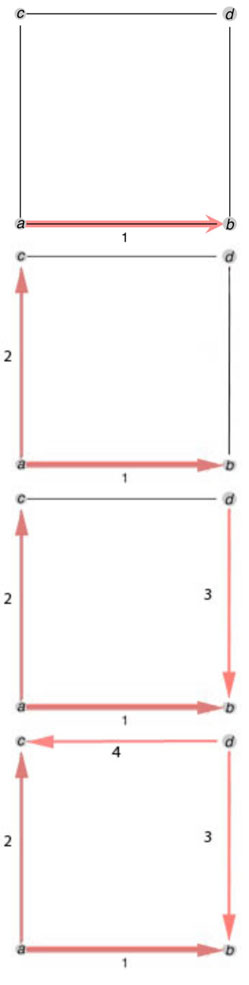
One-tick searching is the fastest way to search graphs, as all searchers can move at one time and search the entire graphs at once. Unfortunately, though, it requires a lot of searchers, especially for large graphs (such as those of cave systems). While this may be the fastest way to find a lost spelunker, it is simply not always feasible – and so a large amount of time is spent looking into two-tick searching.
Two-tick searching
Two-tick searching means that each searcher is allowed to move at most twice. Searchers can begin at any vertex, but can move down only two edges (at the most). This type of searching will also have blockers. The example below is two-tick searching of the 4th order circular graph (C4, a circular graph with 4 vertices).
In this example, the colours indicate the order of the moves; red is the first move and blue is the second. The numbers indicate the searchers; an edge labeled with the number 1 indicates that searcher number 1 moves along that edge and a number 2 indicates that searcher number 2 moves along that edge.
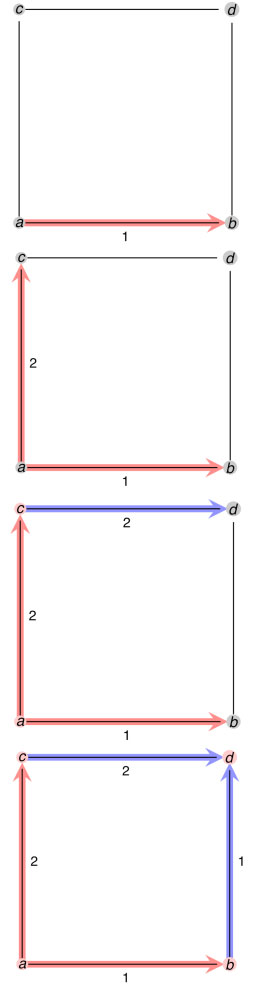
So, under the assumption that searchers number 1 and number 2 can move at the same time, the spelunker could be found in at least two moves.
Within the constraints of two-tick searching, it was discovered that a complete graph of order 6 (K6) could be searched with between 8 and 11 searchers. It was also discovered that the complete 7th order graph (K7) could be searched with between 11 and 14 searchers.
Something not considered in these models is that when a person is actually in a cave, they would be able to see down the corridors as well. It was also not considered that some cave systems have not been mapped out, and rescuers would not know the layout of the system prior to going in for a rescue. In this case, the rescuers would not know how many vertices and/or corridors there would be in the system.
The purpose of this problem was to find a spelunker lost in a cave system, but it is important to keep in mind that there are other applications of this problem. Similar to finding the lost spelunker, we could also find intruders in those networks using similar methods.
