Natasha Glydon
Math and music are usually organized into two separate categories, without obvious overlap. It tends to be that people are good at math and science or art and music, as if the two elements could not be placed together logically. In actuality, math and music are indeed related and we commonly use numbers and math to describe and teach music.
Reading Notes and Fractions
Musical pieces are read much like you would read math symbols. The symbols represent some bit of information about the piece. Musical pieces are divided into sections called measures or bars. Each measure embodies an equal amount of time. Furthermore, each measure is divided into equal portions called beats. These are all mathematical divisions of time.
Fractions are used in music to indicate lengths of notes. In a musical piece, the time signature tells the musician information about the rhythm of the piece. A time signature is generally written as two integers, one above the other. The number on the bottom tells the musician which note in the piece gets a single beat (count). The top number tells the musician how many of this note is in each measure. Numbers can tell us a lot about musical pieces.
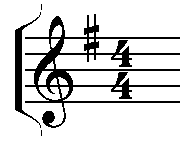 Image reproduced with permission of Neil Hawes |
Each note has a different shape to indicate its beat length or time. Notes are classified in terms of numbers as well. There are whole notes (one note per measure), half notes (two notes per measure), quarter notes (four notes per measure), eighth notes (eight notes per measure), and sixteenth notes (sixteen notes per measure). These numbers signify how long the notes last. That is, a whole note would last through the entire measure whereas a quarter note would only last ¼ of the measure and thus there is enough time for four quarter notes in one measure. This can be expressed mathematically since 4 x 1/4 = 1. A note with a dot after it lengthens the note by half. For example, a quarter note with a dot after it would be held for 3/8
of a measure, since
![]()
Three eigths of a measure is midway between a quarter note and a half note. It is important for musicians to understand the relationships and values of fractions in order to correctly hold a note.
Fibonacci
The Fibonacci sequence is a famous and well-known sequence that follows as: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, … and so on, adding each term to the one before it to create the next term. That is, 5 + 8 = 13, 8 + 13 = 21, 13 + 21 = 34, and continuing infinitely. In music, the Fibonacci sequence can be seen in piano scales. For example, the C scale on the piano consists of 13 keys from C to C; eight white keys and five black keys, with black keys arranged in groups of three and two.
|
In the Fibonacci sequence, the ratio between each term is very close to 0.618, which is known as the golden ratio.
Pythagoras and Frequency
It was Pythagoras who realized that different sounds can be made with different weights and vibrations. This led to his discovery that the pitch of a vibrating string is proportional to and can be controlled by its length. Strings that are halved in length are one octave higher than the original. In essence, the shorter the string, the higher the pitch. He also realized that notes of certain frequencies sound best with multiple frequencies of that note. For example, a note of 220Hz sounds best with notes of 440Hz, 660Hz, and so on.
The closest tie between music and math is patterns. Musical pieces often have repeating choruses or bars, similar to patterns. In mathematics, we look for patterns to explain and predict the unknown. Music uses similar strategies. When looking at a musical piece, musicians look for notes they recognize to find notes that are rare (high or low) and less familiar. In this way, notes relate to each other. Relationships are fundamental to mathematics and create an interesting link between music and math.