Solution to January 2001 Problem

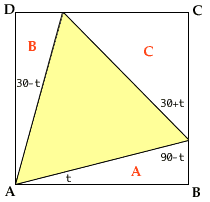
An equilateral triangle is inscribed in, and has a common vertex with, a rectangle. If A, B, C are the areas of the complementary right triangles (as shown in the figure), prove that A + B = C.

This month we received quite similar solutions from Hua Ma (in Computer Science at the University of Regina), Juan Mir Pieras (from Spain), and Midhun Chandran (of the internet). Here is their combined solution.

Letting the angle of region A at vertex A be t, the angles in regions B and C are 30o ± t as indicated in the diagram. Denoting the side length of the equilateral triangle by s, the areas are therefore (using the identity sin 2x = 2 sin x cos x)

4A = 2s2 sin t cos t = s2 sin 2t

4B = 2s2 sin(30o - t) cos(30o - t) = s2 sin(60o - 2t)

4C = 2s2 sin(30o + t) cos(30o + t) = s2 sin(60o + 2t)

Hence, we must show that

sin 2t + sin(60o - 2t) = sin(60o + 2t)

Since sin(60o ± 2t) = sin 60o cos 2t ± sin 2t cos 60o = (sqrt(3)/2)cos 2t ± (1/2)sin 2t,

the left hand side is

(1/2) sin 2t + (sqrt(3)/2)cos 2t ,

which equals the right hand side as claimed.

Comments. The rectangle in the picture looks pretty much like a square, but it really is more general. The ratio of the height AD to the base AB varies from sqrt(3)/2 (when the base of the triangle coincides with AB) to 2/sqrt(3) (when a side of the triangle coincides with AD); that is from approximately 0.866 to 1.155.

Our problem can be traced back to problem 1580 in the Dutch journal Nieuw Tijdschrift voor Wiskunde. That journal published a neat geometric solution from D. Kruyswijk; our solution below is a translation from volume 55 (1967-1968), page 125. To appreciate the solution you must know the following facts about regular hexagons:

  1. A 30o angle is subtended by a side of a regular hexagon at any point of its circumcircle that is not on the short arc determined by that edge.

  2. Each side of a regular hexagon is parallel to a diagonal and half its length.

We wish to show that the areas of the given right triangles A, B, and C satisfy A + B = C. Note that the hypotenuse of each triangle is a side of the equilateral triangle, so they all have the same length. Slide a copy of each triangle around so that its hypotenuse coincides with the segment EF shown on the right side of the accompanying figure, and the vertex with the right angle lies on the upper semicircle. More precisely, slide triangle ABP making A coincide with F, P with E, and similarly for the other two. Next slide a second copy so that the right angle lies on the lower semicircle. Thus B goes to B' and B", C goes to C' and C", and D goes to D' and D". Because the angles in the triangles are t, t ± 30o and t ± 60o, the angles at F that are subtended by successive vertices are all 30o.

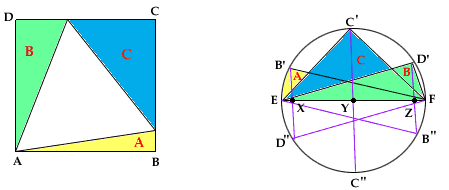
That is, the six points D', C', B', D", C", B" form (in that order) the vertices of a regular hexagon. Denote by X, Y, and Z the points where the segments B'D", C'C", D'B" cross EF. Note that XD" = D'Z and that B'D" and B"D' are parallel to and half the length of C'C". We must show that

Area(EB'F) + Area (ED'F) = Area (EC'F).

This is immediate since all three triangles share the same base, and their heights are proportional to the parallel segments B'X, C'Y, D'Z, while B'X + D'Z = C'Y.