We received four beautiful solutions this month. Here they are, in alphabetical order.
- Solution by Leticia Gimeno (Spain).
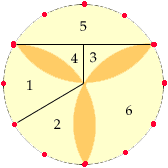
If we draw radii to the points corresponding to 12:00, 8:00 and 4:00, we will obtain six curvilinear triangles, each with a straight side, a concave side, and a congruent convex side. We take an adjacent pair of them (such as pieces 2 and 3) and place them so that the convex arc of one fits into the concave arc of the other: we can that the straight lines of both pieces are parallel. It seems that we've chosen a good way.
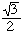 by 3.]
by 3.]
-
Solution by Normand Laliberté (Ontario).
(Translated from the French.)To show: A
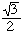 by 3 rectangle can be formed (when the given circle has unit radius).
by 3 rectangle can be formed (when the given circle has unit radius).
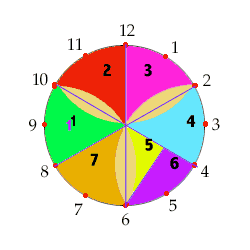
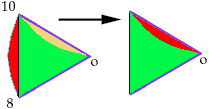
Consider the triangle formed by the center 0 of the circle and the points corresponding to 8 and 12. It is equilateral (because all the angles are 60 degrees). Note that the arc subtended by the chord 8-10 (joining 8 to 10) is congruent to either of the arcs bounding the shaded region split in two by the radius 0-10. Thus, cutting along 8-10 and rotating 60 degrees about the point 10 we can cover half the shaded region with the circular segment, which transforms the curvilinear triangle into a proper equilateral triangle. Its vertices are 0, 8, and 10, its height is
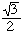 , and its base is 1.
, and its base is 1.
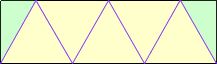
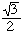 and base is 3.
and base is 3.
- Solution by Juan Mir Pieras (Spain).
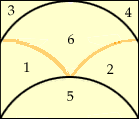
A construction without words! [Note that this rectangle measures
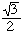 by 3/2.]
by 3/2.]
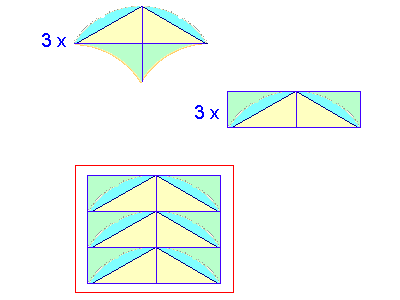
- Solution by Alexander Potapenko (Russia).
Let's connect center of the unit circle to the "even hours" (2, 4, 6, 8, 10, 12). We will obtain 6 sectors, or if we cut off the circular segments -- 6 equilaterial triangles. (A circular segment is a figure bounded by a chord of the circle and the arc it determines.) It's easy to prove that each of these segments we cut off is equal to a shaded segment in each triangle (the same radius and base). Therefore we can put cut segments into shaded ones. So we have transformed our figure into 6 equilateral triangles. It is very easy to combine them into a rectangle - just line them up and bisect one of them (as in solution 2).
Comment. We took March's problem from Which Way Did the Bicycle Go? by J. Konhauser, D. Velleman, and S. Wagon (published by the Math. Association of America) Their published solution uses only six pieces, which is probably the minimum required for a rectangle. It is much like our solution 3, but with fewer cuts: