We shall provide two solutions.
The first is fast but tricky: Count the number of edges around the boundary of your starting configuration of black squares. If you start, for example, with seven black squares, none of which share an edge, the boundary would consist of 7·4=28 edges. If some of the initial squares shared an edge, the boundary would have fewer than 28 edges. The important thing to notice is that the boundary retains the same length when each new black square is added to the previous configuration: two edges are added to the new boundary, while two edges are lost from the old, namely the two that neighboured the new square. (To see how this works, note that in both parts of the above figure there are eight edges on the boundary of the black region both before and after blacking in the square labeled X.) Of course, the entire 8 by 8 grid has a boundary of 32 edges, so one must start with a configuration of at least eight black squares, no two of which share an edge.
The alternative solution is harder to explain in complete detail, so only an outline will be given. Starting with any j by k black rectangle, we fill in a larger black rectangle in one of three ways:
Any j by k black rectangle that has a black square attached at one of the four vertices will be completed to a (j+1) by (k + 1) rectangle.
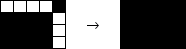
If a j by k rectangle has been blackened and there is a black square adjacent to the side with j squares, the new squares that get filled in will produce a j by (k+1) blackened rectangle.
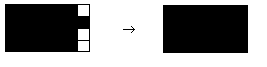
If a j by k rectangle has been blackened and there is a black square having a neighbouring white square adjacent to the side with j squares, the new squares that get filled in will produce a j by (k +2) blackened rectangle.
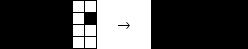
Thus, each new black square adds at most one new row and one new column, or at most two rows, or at most two columns. Suppose we begin with an initial configuration of only seven black squares. Choosing one of them to start the process, we would have 7 rows to fill and 7 columns, but only 6 squares to work with, which (growing two at a time) can fill at most 12 of the remaining 14.