A regular tetrahedron is a pyramid that consists of four
equilateral triangles, each joined to the other three along their sides.
The resulting six edges, consequently, all have equal lengths. Imagine
that on each of the four faces, a car is traveling in a clockwise direction
at a constant speed along the edges bounding that face. Each of the four
cars may be traveling at a different speed and may start anywhere on the
boundary of its face. Can the cars always keep from crashing, or is there
destined to be a collision along some edge?
We received similar solutions from Juan Mir Pieras (Spain) and Alexander Potapenko (Russia). We shall begin with Potapenko's solution.
Not even three cars can avoid a collision. Let's denote the tetrahedron's vertices by A, B, C, D. Then, as in the figure, three cars will travel the paths ABC, ADB, BDC. Let's name these cars LEFT, RIGHT and DOWN respectively.
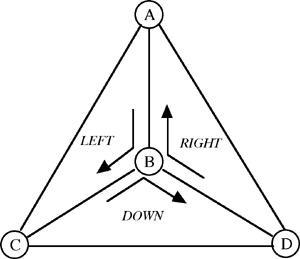
One of the cars will have the minimum speed. (If 2 or 3 cars have the minimum speed take any of them). Let it be the DOWN car. We examine the moment when this car is located at B (and travelling toward D).
Where can the RIGHT car be located? Of course it cannot be on BD, because of inevitable collision with the DOWN car.
It can't be on AD either - because of its greater speed it will reach D before (or at the same time as) the DOWN car and collision on BD will be inevitable.
Similarly we can prove that the LEFT car can't be at BC or AC. The easiest way to do it Ñ run the picture in reverse. If forward motion runs without collisions, then the reversed picture will likewise be without collisions. For the DOWN car in reversed motion, the LEFT car looks like RIGHT car in did in forward motion, so positions on BC and AC are forbidden.
So we can see that both for LEFT and RIGHT cars to avoid collisions with the DOWN car, they must be on AB and a collision between them is inevitable. (Note that it does not matter which of them arrived on AB first Ñ a collision will be in the near future or was in the near past.) This completes the proof that with any three of the cars a collision is inevitable.
Comments.Although the mathematical argument above is convincing, a skilled lawyer might still be able to argue the case that there is a way to avoid collisions: if all cars were to move at zero velocity there would be no collisions at all. Indeed, this seems to be a good way to eliminate the world's traffic problems Ñ just make a law that everyone must keep his car parked all day. On the other hand, both solvers suggested modified versions of the problem that allow nontrivial ways to avoid collisions.
Potapenko observed that were two cars, for example ABC and ADB, to travel clockwise, and two, BCD and ADC, to move counterclockwise, then it can easily be arranged for the cars to avoid one another. With these new directions for motion and the same speed for all four cars, we have two independent conflict pairs (where the same direction is a conflict). Cars in a pair can move by a simple rule: when one car is in the middle of the common edge the other is at the opposite vertex. In fact, in Italy drivers use their own version of this solution: Drivers there often travel on the wrong side of the road and occasionally go the wrong way down one-way streets (at high speed) just to avoid collisions. They also drive their cars on the sidewalks, presumably for the same reason.
Mir's solution made use of explicit models. One nice consequence of that approach is the natural generalization of the problem to allow cars to pass at a vertex. (I personally would not like to be in one of the cars that arrived at an intersection at the same time as a car coming from the side; however, this is mathematics, not physics, so we are permitted to investigate a modified problem if we wish.) With three cars moving at the same speed and one at exactly half that speed, there is a solution. An easy way to describe it is to label the edges 1 through 6 as in the figure.
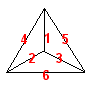
For the solution we display the edge traveled by the respective cars during given units of time.
| LEFT | ... | 1 | 2 | 4 | 1 | 2 | 4 | ... |
| RIGHT | ... | 5 | 3 | 1 | 5 | 3 | 1 | ... |
| DOWN | ... | 3 | 6 | 2 | 3 | 6 | 2 | ... |
| BACK | ... | 4 | 4 | 6 | 6 | 5 | 5 | ... |
Observe that no column has a repeated edge number, which we interpret as telling us that no two of the four cars are on the same edge at the same time. Note, however, that each car meets the other cars at a vertex in agreement with the solution to the original problem. Mir proves that a solution is likewise possible when there is one fast car and three travelling at half that speed, but no other combination of speeds admit a solution to this generalized problem.
The source of our February problem was number 130 from the problem-of-the-week web page of Alberto Delgado at Bradley University (Peoria, IL): http://bradley.bradley.edu/~delgado/potw/potw.html
His source of the problem was his colleague, Tony Bedenikovic. Professor Delgado kindly provided the following background.