Complete the following sentence by filling in each blank with a numeral of one or more digits.

Solution to MP28

We received solutions from Neil Chatani (California), Pierre Bornsztein (France), Juan Mir Pieras (Spain), and Gordon Robinson (British Columbia). Robinson, our correspondent, is apparently not related to the person who devised MP28, except perhaps in spirit. Raphael M. Robinson (1911-1995) was a versatile mathematician who contributed greatly to the reputation of Berkeley's mathematics department. In addition to his important work in logic, number theory, and many other fields, he always maintained an interest in recreational mathematics, devising and solving interesting problems at all levels of sophistication. Gordon Robinson correctly pointed out that our statement of R.M.'s problem is ambiguous; there are more than two solutions depending on how one interprets the sentence. We should have made explicit that the numbers that appear are themselves digits -- more about that later.

With our intended interpretation of Robinson's sentence, the possible ways to complete it are

First way: In this sentence, the number of occurrences of 0 is 1, of 1 is 7, of 2 is 3, of 3 is 2, of 4 is 1, of 5 is 1, of 6 is 1, of 7 is 2, of 8 is 1, and of 9 is 1.

Second way: In this sentence, the number of occurrences of 0 is 1, of 1 is 11, of 2 is 2, of 3 is 1, of 4 is 1, of 5 is 1, of 6 is 1, of 7 is 1, of 8 is 1, and of 9 is 1.

The first solution is perhaps the most natural, where all the entries are digits. To see that it is the only answer of this kind, it is perhaps best to consider the graph obtained by putting an arrow from x to y if in the sentence, the number of occurrences of x is y.

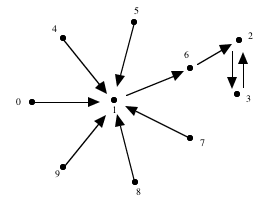
In this graph, the digits with arrows pointing to 1 are precisely those with no arrows pointing into them, while the digits with arrows pointing to 2 are precisely those with one arrow pointing to them. More generally, there is an arrow x -> y if and only if y is one plus the number of arrows that point to x. Also, there is a path 1 -> x₁ -> x₂ -> ... starting at 1. Because there is a finite number of digits, this path must eventually create a cycle when one element x_j will point to an earlier encountered element xi. In fact the component containing 1 has nothing else than the arrows pointing to 1 and the path looping into itself. Indeed, starting from the cycle and backtracking along arrows, we must always reach a dead end -- a digit pointing to 1.

Now, consider the path starting at 0: We have 0 -> 1 -> x. Since x has an arrow pointing to it, x cannot be 1; nor can x be 2, which is easily seen: for example, there is also an arrow from 9 to 1 (because no digit could occur exactly nine times). Therefore we have x -> 2, and 2 -> y -> 2, thus y = 3. The other elements in this component all have arrows pointing to 1. In fact, at this point we can show that there are no other components: Indeed, in any component there is exactly one arrow coming out of every vertex, so there is an average of one arrow coming into every vertex. Consequently, there must be a vertex with at most one arrow coming into it, so this vertex is in the component of 1 and 2. Thus the graph is connected, and it has the six remaining digits pointing to 1. The first solution is deduced from this graph structure.

We pause briefly to consider a version of Robinson's sentence involving Roman numerals:

The number of occurrences of (uppercase) I is IX, of V is I, of X is II, of L is I, of C is I, of D is I and of M is I in this sentence.

Among other things, this shows that the number of ways to complete the sentence depends on the system of numbers that we are using. The second way to complete Robinson's sentence depends heavily on the fact that we are counting in base 10. Here is Gordon Robinson's argument:

We let n(d) be the number of occurrences of the digit "d". It is fairly clear that there cannot be an n(d) ≥ 20, nor more than one n(d) ≥ 10 since the total number of digits implied grows more quickly than the number of digits in the sentence. So there must be at most one n(d) greater than 9 but less than twenty. In this case, the sum of the numbers in the blanks equals 21.

Again here it is clear that n(1) must be the large number. Now there is an additional one coming from the second digit of n(1). However, in order for there to be that many ones, almost all the other n(d) must be one. If they all were, then there would be at least 10 plus the number of 1’s in n(1), which is at least one. But if n(1) = 11 then not every other n(d) can be 1, since now there would be 12 1’s. Since sum of the numbers in the blanks equals 21, and each n(d) ≥ 1, n(d) must be less than or equal to 12. But if n(1) = 12, there are not enough places to locate all the required 1’s (only 9 blanks remain and ten 1’s are required). So the only possibility is that n(1) = 11. To remedy the problem that we might have two many 1’s, we can set n(2) = 2 eliminating one 1 and supplying the necessary 2 to make up the two now required. So the second solution is:

n(d) = 1 for d = 0, 3, 4, 5, 6, 7, 8, 9

n(1) = 11

n(2) = 2.

However, there is an issue of interpretation as noted above. In fact, in reading my argument in the previous paragraph, it should be noticed that there are a number of places where numbers were written out in words. The issue is around how we interpret the meaning of the symbols 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 in the original uncompleted sentence. The solution above views them as digits. However, if we view them as numbers, the solutions are different. The first solution is still valid because the blanks are all filled with one digit numbers and so the count remains unchanged. However, the second solution depends on counting digits. If we count these symbols as numbers, the following solution occurs:

N(k) = 1 for k = 0,2,3,4,5,6,7,8,9

N(1) = 10 (noting that the number 10 does not enter into the counting at all!).

Gordon goes on to give another interpretation. Instead, let us modify the statement of the problem to make it explicit that each numeric symbol that occurs represents a digit. Revised problem:

In this sentence, the number of occurrences of the digit "0" is ____, of "1" is ____, of "2" is ____, of "3" is ____, of "4" is ____, of "5" is ____, of "6" is ____, of "7" is ____ of "8" is ____, and of "9" is ____.