Solution for January 2011

The Problem:
	Heron's formula tells us that the area of a triangle is determined by the lengths of its three sides; is it true that the volume of a tetrahedron is determined by the areas of its four faces?

Correct responses:
	Correct solutions to the January problem were submitted by Claudio Baiocchi (Italy) Benoît Humbert (France) Lou Cairoli (USA) Ile Ilijevski (Macedonia) Mei-Hui Fang (Austria) Wolfgang Kais (Germany) Philippe Fondanaiche (France) John T. Robinson (USA) Bruce Golfman (Austria) Albert Stadler (Switzerland) Verena Haider (Austria)

The solution:

The short answer is that no, the volume of a tetrahedron is not determined by the areas of its four faces. For a simple counterexample, which was provided by about half of our correspondents, compare the regular tetrahedron, scaled so that each face has unit area, to the square, scaled so that its area is 2: The regular tetrahedron has a positive volume, while the square $ABCD$ is a degenerate tetrahedron whose faces $ABC, BCD, CDA, DAB$ likewise all have area 1, but its volume is 0. This tells us that a Heron-like formula would be impossible because it would have to provide the same value for the volumes of these two tetrahedra.

For those readers who are unhappy with the use of degenerate figures, we can easily provide a more satisfying solution. We first review some basic facts about tetrahedra; these properties are discussed on many web pages (Wikipedia, for example), where ample standard references for their proofs have been provided.
All of the submitted solutions dealt with isosceles tetrahedra, whose four faces (by definition) all have the same area. These have particularly nice properties, which are summed up by the following theorem:


Theorem. If a tetrahedron satisfies any one of the following six properties, then it is isosceles and it satisfies all six properties.

1. All four faces have the same area.
   
   
2. All four faces have the same perimeter.
   
   
3. All four faces are congruent.
   
   
4. Opposite edges are equal.
   
   
5. The face angles of the three faces at any vertex sum to $180^\circ$.
   
   
6. The insphere and circumsphere have the same center.

As in Baiocchi's solution, it follows that a model of an arbitrary isosceles tetrahedron can be constructed from a plane triangle by using as base its medial triangle (whose vertices are the midpoints of the given triangle) and folding up the other three congruent triangular pieces: fold along the dashed lines in the triangle on the left of the accompanying figure to get the tetrahedron on the right.

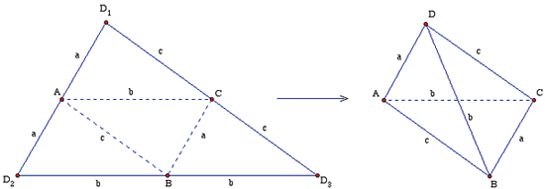
Figure 1: An isosceles tetrahedron with edge lengths $a, b$, and $c$.

We can further simplify our task by setting $a=b$, so that each face of our tetrahedron becomes an isosceles triangle with side lengths $a,a,c$ and area
$$A=\frac{c\sqrt{4a^2 - c^2}}4.$$
(For the source of this formula and that of the volume that follows, see the short appendix at the end.) If we set $A=1$ and allow $c$ to vary, then
$$a=\sqrt{\frac{c^2}4 + \frac4{c^2}}\;,$$
and the volume of the tetrahedron in terms of the side length $c$ will be
$$V = \frac{c^2}{\sqrt{72}}\sqrt{\frac8{c^2}-\frac{c^2}2}.$$
One sees that the volume approaches 0 as the length $c$ shrinks to 0 or approaches $2$ (where the tetrahedron degenerates to a square); between these two extremes the volume is positive, increasing to its maximum at $c = \frac2{3^{1/4}}\approx1.52$ (where the tetrahedron is regular).

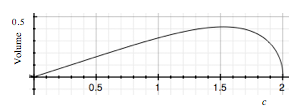
Figure2: Volume of an isosceles tetrahedron as a function of $c$ when
          its faces have unit area and edge lengths $a, a$, and $c$.

An alternative approach.
Several solvers used vectors for their solution. We can let the vertices of our isosceles tetrahedron have coordinates
$$(0,0,0),\quad (a,b,0), \quad (0,b,c), \quad \mbox{ and } \quad (a,0,c).$$
Note that the side lengths indeed come in pairs, namely $\sqrt{a^2+b^2}, \sqrt{b^2+c^2}$, and $\sqrt{a^2+c^2}$. The standard vector formulas for volume and area give us
$$V = \frac16\left|\begin{array}{ccc}a & b & 0 \\0 & b & c \\a & 0 & c\end{array}\right| = \frac13 abc,
\quad \mbox{ and } $$ $$ \quad A = \frac12 \left |\left(\begin{array}{c}a \\b \\0\end{array}\right) \times
\left(\begin{array}{c}0 \\b \\c\end{array}\right)\right | = \frac12 \sqrt{(ab)^2 + (bc)^2 + (ca)^2} .$$
Again here we can simplify our task by setting $a=c$.

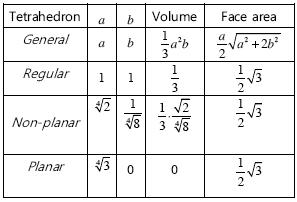
Figure 3: Golfman's table of volumes and face areas of tetrahedra whose
     vertices are $(0,0,0), (a,b,0), (0,b,a)$, and $(a,0,a).$

Comments. Our January problem was taken from the 1983 Canadian Mathematical Olympiad, proposed by John Wilker. Cairoli found a number of interesting references that dealt with closely related issues. It might seem plausible that there would exist at most one tetrahedron when its volume is specified as well as its four face areas. But no, Lisoněk and Israel showed that the tetrahedron might not be unique even with a specified circumradius [Petr Lisoněk and Robert B. Israel, Metric invariants of tetrahedra via polynomial elimination. C. Traverso, Ed., Proceedings of the 2000 International Symposium on Symbolic and Algebraic Computation, ACM Press (2000) pp. 217-219]. In fact there exists an infinite family of noncongruent tetrahedra having the same volume, circumradius, and face areas [Lu Yang and Zhenbing Zeng, An open problem on metric invariants of tetrahedra. M. Kauers, Ed., Proceedings of the 2005 International Symposium on Symbolic and Algebraic Computation, ACM Press (2005) pp. 362-364]. On the other hand, C. -S. Lin in [The Volume of a Tetrahedron and Areas of its Faces. Crux Math. with Mayhem, 27:3 (April 2001) 207-212] discussed a variety of families of tetrehedra whose volumes are determined by their face areas. One such example is what he calls a ''Heron tetrahedron", which is a tetrahedron with at least one pair of faces that meet at right angles. (But beware of the misprint there: the half was omitted from the formula for $s$, which should have been $s=\frac{1}{2}(a+b+c+d)$.)

Appendix. The Cayley-Menger determinants give the volume of a simplex in $n$-dimensional space in terms of its side lengths. We used two cases in our discussion of areas and volumes. In two dimensions, the area $A$ of a triangle whose sides have lengths $a,b$, and $c$ satisfies
$$-16 A^2\left|\begin{array}{cccc}0 & 1 & 1 & 1 \\1 & 0 & c^2 & b^2 \\1 & c^2 & 0 & a^2 \\1 & b^2 & a^2 & 0\end{array}\right| = (a+b+c)(-a+b+c)(a-b+c)(a+b-c)\;,$$
which we recognize as Heron's formula.

In three dimensions we label the edge lengths of one face $a,b$, and $c$, and the edges opposite them $a',b'$, and $c'$, respectively. The volume $V$ satisfies
$$288V^2 = \left|\begin{array}{ccccc}0 & 1 & 1 & 1 & 1 \\1 & 0 & c^2 & b^2 & a'^2 \\1 & c^2 & 0 & a^2 & b'^2 \\ 1 & b^2 & a^2 & 0 & c'^2 \\1 & a'^2 & b'^2 & c'^2 & 0\end{array}\right| \;.$$
A simple proof of the formula and a discussion of its history can be found in [Reuben Hersh, College Math. J., 35:2 (March 2004) 112-114].
It is equivalent to the formula associated with the name Tartaglia (1500(?)-1557), although it was evidently discovered a century before him by the early Renaissance artist Piero della Francesca (1420(?)-1492). Note that for an isosceles tetrahedron $a=a', b=b', c=c'$. These determinants further reduce to the area and volume formulas we gave earlier when we set $a=b$.