| |||
| Math Central | Quandaries & Queries |
|
Question from Rahul, a student: How do i find the volume of a sphere without the knowledge of calculus? |
There is a classic Greek proof, which does not explicitly use calculus.
[Calculus as we know it was created much later.]
The secret is this:
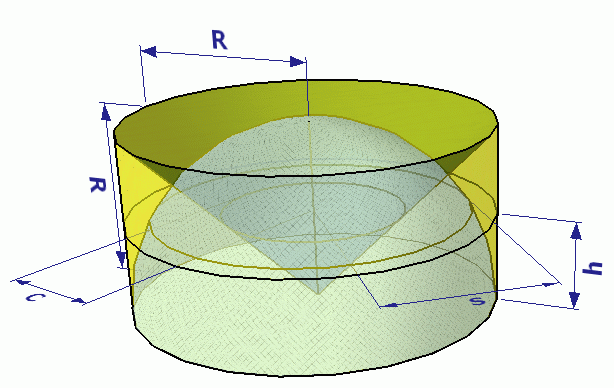
Take a hemisphere.
Surround it by a cylinder of the same radius as the hemisphere,
and the height of the hemisphere (the radius again). We assume you know the volume of
a cylinder.
(π R2) (R) = (Area of base) x height.
Now, take an inverted right circular cone in the cylinder. with the flat 'base' of the cone at the top of the cylinder, and the point at the bottom (at the center of the hemisphere). We assume you know the volume of a cone:
(1/3) (area of base) x height = (1/3)(π R2)(R)
Now you have this:
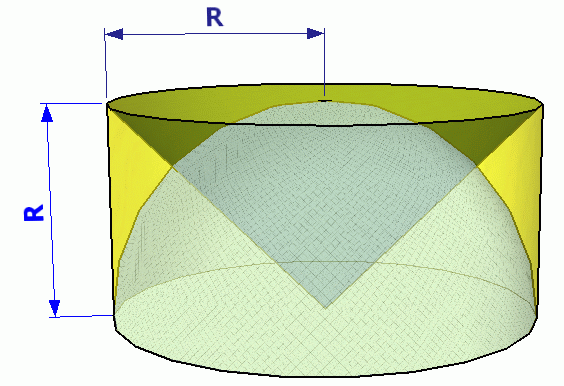
Proposition:
On any horizontal slice of this configuration, the area of the cross section of the hemisphere equals the area of the cross section of the cylinder minus the area of the cross section of the inverted cone.
Proof:
This just involves writing out the areas of the three different circles and seeing that the way the radius of the circular cross section of the hemisphere changes and the way the cross section of the cone changes match up.
Take an arbitrary horizontal slice at distance h above the flat base of the hemisphere. Clearly, the cylinder's circular slice is the same throughout: it has an area of πR2.
The area of the circular cross-section of the cone is πC2, where C is the radius of the cone at this point. The area of the circular cross-section of the hemisphere is πS2, where S is the radius of the hemisphere at this point. Let's look at the two dimensional geometry:
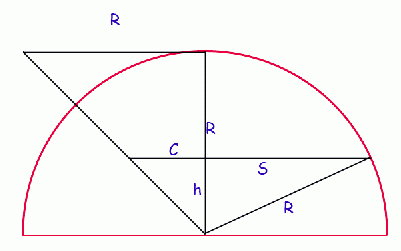
Clearly, the cone is an isosceles triangle (two sides = R) and so the smallest triangle is similar to the cone, so C = h. As well, the sides of h, S, R make a right triangle, so Pythagoras tells us that S2 + h2 = R2.
Thus, πC2 + πS2 = πh2 + π(R2 - h2) = πR2, so we have proven our proposition.
Conclusion (General principle):
If two solids have cross sections of equal area for all horizontal slices, then the have the same volume.
Therefore the volume of the hemisphere
= volume of cylinder - volume of cone
= (π R3) - (1/3) (π R3)
= (2/3) (π R3)
The volume of the sphere is twice that. So it is (4/3)(π R3).
One neat feature of this approach is that it DOES lead to a general method which WILL be used later in calculus - the so called 'slab method' for finding volumes.
Walter Whiteley and Stephen La Rocque.
 |
||
| * Registered trade mark of Imperial Oil Limited. Used under license. | ||
Math Central is supported by the University of Regina and the Imperial Oil Foundation.