Hi, my name is Jessica, 7th grade, and Im doing a Math Fair project on optical illusions. As one of the required factors, we need a "mathmatical significance" paragraph. Unfortunatley, I can only think of one way that optical illusions have to do with math, and thats time because some optical illusions tell you to look at the picture for a certain amount of time. Please help me, I would be grateful beyond words.
Thanks! ~*Jessica*`
Hi Jessica,I'm not sure about "mathematical significance" but I can show you some ways that mathematical concepts can help explain optical illusions.
I found a web site called IllusionWorks that has some interesting optical illusions but what I want to point out are two quotes from their page Introduction to Illusions. The quotes are
This seems to be the source of some optical illusions. We see a two dimensional image on a page and our brains constructs a three dimensional image that may be an impossible object.
Let my try to illustrate with an example from a fasinating book I just read. The book is
Look at the three illustrations
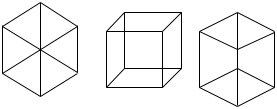
Your brain probably constructs a three dimensional cube from the image in the center but the images on the left and right look flat.
Hoffman uses mathematical concepts to try to explain how our brains construct the images we see. He calls them rules.
Rule 2. If the tips of two lines coincide in an image, then always interpret them as coinciding in three dimensions.
So, for example in the image on the left, the diagonal lines intersect in the image and hence your brain uses rule 2 to construct a three dimensional image where these lines intersect, forcing it to be flat.
The "optical illusion" where this can be seen is the devil's triangle or impossible triangle.
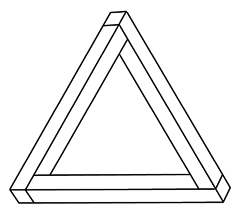
Rules 1 and 2 force you brain to try to construct a three dimensional object where lines in the image are lines in three dimensions, and coinciding lines in the image are coinciding lines in three space. However a different image shows that your brain might be using the rules to construct the wrong object.
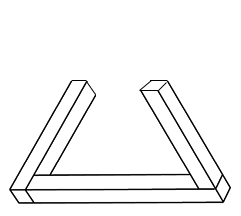
This is two sticks lying an a table and the third stick, on the right, standing vertically. Now move your head to the right until the top end of the vertical stick coincides with the far end of the stick on the table. What you see is the impossible triangle.
I hope this helps,Penny