| |||
| Math Central | Quandaries & Queries |
|
Question from lil, a student: Why are repeating decimals considered rational numbers? |
We have two responses for you
Hi Lil,
The answer is yes, but before I illustrate why I am going to quibble with the way you asked the question. A repeating decimal is not considered to be a rational number it is a rational number. We have different ways of representing numbers, for example the number of fingers on my left hand can be represented by the English word five, or the French word cinq or the symbol 5 or the Roman numeral V or the fraction 10/2 or many other ways. Similarly the fraction 1/3 can be represented by the decimal number 0.3333... These are two different ways of representing the same number.
A rational number is a number that can be represented a/b where a and b are integers and b is not equal to 0.
A rational number can also be represented in decimal form and the resulting decimal is a repeating decimal. (I see the decimal 0.25 as repeating since it can be written 0.25000...) Also any decimal number that is repeating can be written in the form a/b with b not equal to zero so it is a rational number. Let me illustrate with an example.
Consider the repeating decimal n = 2.135135135... The repeating part (135) is 3 digits long so I am going to multiply n by 103 to get 103 n = 2135.135.135... Now I subtract
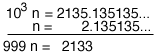
Thus n = 2133/999 and since 9 divided both the numerator and denominator this can be written
n = 237/11.
Penny
Hi there,
Repeating decimals are considered rational numbers because they can be represented as a ratio of two integers.
To represent any pattern of repeating decimals, divide the section of the pattern to be repeated by 9's, in the following way:
0.2222222222... = 2/9
0.252525252525... = 25/99
0.1234567123456712345671234567... = 1234567/9999999
The number of 9's in the denominator should be the same as the number of digits in the repeated block. These rational numbers may of course be reducible, if the top is divisible by 9, or both the top and bottom are divisible by another number. But this is a starting point which will always get you what you want.
Why does this work? Well, we can go into a bit more detail and write out our repeating decimal, say 0.252525252525..., as an infinite series of decreasing fractions, like so
0.252525252525... = 2/10 + 5/100 + 2/1000 + 5/10000 + 2/100000 + 5/1000000 + ...
Now let this series be equal to x, that is
x = 2/10 + 5/100 + 2/1000 + 5/10000 + 2/100000 + 5/1000000 + ...
now multiply both sides by 100
100x = 20 + 5 + 2/10 + 5/100 + 2/1000 + 5/10000 + ...
Now subtract the 1st equation from the second like so:
100x = 20 + 5 + 2/10 + 5/100 + 2/1000 + 5/10000 + 2/100000 + 5/1000000 + ...
-x = - 2/10 - 5/100 - 2/1000 - 5/10000 - 2/100000 - 5/1000000 - ...
--------------------------------------------------------------------------------------------------------------------
99x = 25
now rearrange for x and get
x = 25/99
which is what we were looking for! So 25/99 really does equal 0.252525252525...
I hope this helps!
Gabe
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.