A geometric view of the square root algorithm
A. Grzesina
St. Mary's school
Regina, Saskatchewan
There are two facts concerning the square of an integer that are useful
in the inverse process of finding the square root. The first concerns the
number of digits. In short:
If 0 < a < 10 then 0 < a2 < 100,
if 10 < a < 100 then 100 < a2 < 10 000,
if 100 < a < 1000 then 10 000 < a2 < 1 000 000,
.
.
.
The point to see here is that the square of an integer has either twice
as many digits as the integer itself, or one less than twice as many. So,
since 9,409 has 4 digits its square root has 2 digits, and the square root
of the 13 digit number 3,871,696,594,290 has 7 digits.
The second fact concerns the "geometry" of squaring a number.
Consider, for example, the square of 249 so the geometric object to consider
is a square with side of length 249 units. Write 249 as 200 + 40 + 9 then
the square can be seen as
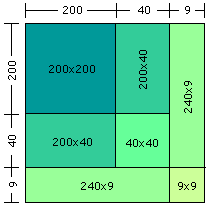
and the square of 249 is 200x200 + 2(200x40) + 40x40 + 2(240x9) + 9x9
= 62001.
Now to find the square root of an integer you need first to determine the
number of digits there will be. Let us find the square root of 64 009. Since
64 009 has 5 digits, the square root of 6 | 4 0 | 09 will have 3 digits.
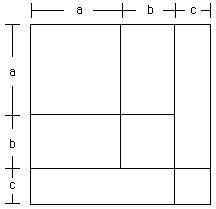
First recall some of the geometric detail of a 3 digit number.
A square of a 3 digit number is divided into 7 parts as shown in the diagram.
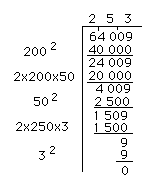
|
To find the square root of 64 009 we will start with the group of digits furthest to the left. We will therefore start with the group whose only member is 6. This represents the square of a. We know that the largest perfect square less that 6 is 4, and that the square root of 4 is 2. Since 2 must be placed in the hundreds position, we know that a = 200. The area of region 1 is 200x200 = 40 000. We then subtract this area from the total area of 64 009. By looking at the diagram we realize that next we should remove the areas of the two regions whose sides are a and b. To find the length of b we must estimate the quotient of 24 009 by 400. The 400 is arrived at by recalling that two regions, each of which has a length of 200, would have an overall length of 2(200) = 400. |
The quotient of 24 009 by 400 is approximately 60. However. looking again at our diagram we realize that besides the two areas of a x b, we also must subtract an area of b x b. Since 2 x 200 x 60 = 24 000 we are left with only 9, but we need to subtract b x b which is 60 x 60 = 3 600. Thus we reduce our estimate of b to 50, and place a 5 in the tens position of the square root calculation. Two rectangles, each 200 units by 50 units, have a total area of 20 000 square units. Subtracting 20 000 from 24 009 leaves 4 009. Again, going back to the diagram we note that the area of b x b that must be subtracted is now 50 x 50 = 2 500. Subtracting 2 500 from 4 009 leaves 1 509.
Returning to the diagram we note that next we must subtract the areas of the two regions which has a length of a + b = 250 units each. The unknown quantity c can now be estimated by the quotient of 1 509 by 500. 500 is arrived at by placing the two regions together to arrive at a rectangle with length 2 x 250 = 500. The quotient of 1 509 by 500 is approxiamtely 3. Place 3 in the units position of the square root calculation and subtract the sum of the areas of regions 5 and 6 , which is 2 x 250 x 3 = 1 500. Subtracting 1 500 from 1 509 leaves 9. From the diagram the rregion 7 is the only region not subtracted so far and its area is c x c = 3 x 3 = 9. Subtracting 9 from our previous remainder leaves us with a remainder of 0. Thus the square root of 64 009 is 253.
To return to the previous page use your browser's back button.