Denis Hanson, Department of Mathematics & Statistics, University of Regina

Diane Hanson, Saskatchewan Education (O.M.L.O.), Regina, Saskatchewan

1. Introduction

Le National Council of Teachers of Mathematics déclare: " ... que tous les élèves ont besoin d'apprendre plus de mathématiques, souvent de façon différente, et que les approches pédagogiques doivent être révisées." ([1], page 1). Afin que la population générale puisse faire face aux besoins d'un monde changeant, les buts généraux des programmes d'études de mathématiques doivent préparer les élèves de façon à: développer les habiletés et la connaissance de concepts nécessaires au consommateur averti; développer l'habileté à analyser et interpréter de l'information; développer la pensée logique et une appréciation des mathématiques; développer le désir, la confiance et l'habileté à résoudre des problèmes; communiquer en langage mathématique; et poursuivre des études avancées en mathématiques ou d'autres domaines d'études reliés aux mathématiques. (voir [3], page iii). C'est par l'entremise de ces buts généraux que les élèves obtiendront une culture étendue des concepts mathématiques. Mais afin d'atteindre ces buts, "la résolution de problèmes doit être le point central du programme d'études de mathématiques. (Elle) doit imprégner tout le programme et offrir le contexte pour l'acquisition de concepts et d'habiletés." ([1], page 23). Ces sentiments sont réitérés dans Mathematics, Charting the Course, Summary and Recom- mendations, [4].

"A cette fin, nous voyons les salles de classe comme étant des endroits où, régulièrement, l'on explore des problèmes intéressants contenant des idées mathématiques importantes. Nous croyons fortement que ce que l'élève apprend est énormément influencé par comment l'élève l'a appris... ." ([1], page 5). Les élèves doivent avoir l'opportunité de modeler et résoudre quotidiennement des problèmes tirés de la vie courante; c'est par cet apprentissage actif que les élèves développent une appréciation du processus de la résolution de problèmes. "Les mathématiques deviennent utiles pour les élèves seulement quand elles sont développées par l'entremise d'un engagement intellectuel personnel qui crée une compréhension nouvelle." [2].

Dans cet article, nous utilisons un problème provenant des mathématiques discrètes. Bien que les "Standards" du N.C.T.M. recommandent que cette branche des mathématiques (le dénombrement, les permutations, les combinaisons, la théorie des graphes, etc.) soit enseignée au niveau secondaire, maints exemples se prêtent au niveau intermédiaire (et même au niveau élémentaire!). Dans l'exemple ci-dessous, nous partons d'une situation familière à l'élève pour arriver au modèle mathématique. Un des avantages de cette activité est qu'il n'y a pas de solution unique. Trouver diverses solutions demande que les élèves aient une bonne compréhension du problème, et les différentes façons de solutionner le problème accordent une opportunité idéale pour la discussion en classe. Le problème et les concepts peuvent être facilement adaptés à d'autres situations réelles. Nous conclurons avec d'autres problèmes qui peuvent être modelés de façon semblable.

2. Le problème.

Il y a eu une grosse tempête de neige et toutes les rues sont fermées. On suppose que toi et tes amis(es) avez une carte montrant toutes les routes entre vos maisons et en plus, vous connaissez le nombre de minutes que prend le chasse-neige pour nettoyer chacune de ces routes. Votre problème est de trouver le parcours à suivre par le chasse-neige afin que celui-ci nettoie juste assez de rues pour que chaque camarade puisse se rendre de sa maison à celles des autres, et que ce parcours prenne le moins de temps possible. Pour aller d'une maison à n'importe quelle autre maison, on peut certainement passer devant toute autre maison.

3. La mathématique.

Nous voulons aborder ce problème de façon intuitive et éviter les définitions et preuves formelles. Cependant quelques définitions aideront à solutionner le problème. En mathématique discrète, un graphique ou un réseau est un ensemble de sommets et d'arêtes qui joignent des paires de points. Parfois nous donnons aux arêtes des valeurs qu'on nomme leurs poids. Un réseau est connecté si on peut aller d'un sommet à n'importe quel autre sommet en passant par ou "marchant sur" les arêtes. La figure 1 est un exemple d'un réseau connecté avec 9 sommets et 16 arêtes. (Nous nous restreignons aux cas où les arêtes ne se croisent pas et ainsi restons avec des figures planes).

Un Graphique ou Réseau

Figure 1

Un Arbre

Figure 2

4. Le modèle et la solution.

Comme modèle pour notre problème, nous nous servons du réseau avec poids de la figure 3, dans lequel les sommets sont les maisons, les arêtes correspondent aux routes et les poids sur les arêtes sont les nombres de minutes requises pour nettoyer les routes. Pour résoudre le problème les élèves ont besoin de noter certaines observations. Les élèves doivent se souvenir que toutes les maisons doivent être connectées. Pour accomplir cette tâche de façon efficace, les élèves doivent construire un arbre qui connecte les maisons de façon à ce que le poids total des arêtes de l'arbre soit aussi petit que possible. Le poids total de l'arbre représente le temps requis par le chasse-neige.

La raison pour laquelle un arbre est la solution idéale est que si on a un cycle, on peut toujours éliminer une des routes de ce cycle et encore garder toutes les maisons connectées (avec moins de travail pour le chasse-neige). L'algorithme qui résout ce problème (et s'appelle l'algorithme de Kruskal, voir [5], à la page 54) est un exemple d'un algorithme dit "avare" - on sélectionne les routes de la façon la plus avare possible.

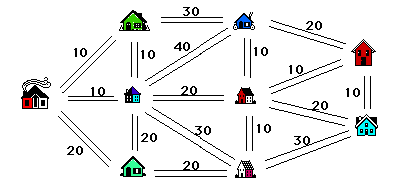
Figure 3

C'est évident que l'on désire choisir des routes avec les plus petits poids possible. Si on choisit toutes les routes avec le plus petit poids (toutes les routes de poids 10 dans notre exemple), nous aurons aussi des cycles, alors nous en choisissons autant que possible sans créer de cycles. Il n'y a pas de façon unique de faire cette sélection. Ensuite, nous choisissons des routes de poids 20, encore en évitant de créer des cycles. On continue de cette façon jusqu'à ce qu'on aie sélectionné une route de moins que le nombre de maisons (dans notre exemple, 8 routes). Le résultat est un arbre avec un poids total (temps) minime. Deux solutions sont illustrées dans la figure 4. Il est à noter que, bien que les solutions soient distinctes, le poids total des arêtes choisies est le même dans les deux cas (10 + 10 + 10 + 10 + 10 + 10 + 20 + 20 = 100 minutes). Ceci est toujours le cas quelle que soit la solution.

Combien d'autres solutions différentes peux-tu trouver?

5. Directions futures et problèmes.

Les concepts rencontrés peuvent être utilisés dans une foule d'autres applications. Un réseau devient un modèle mathématique pour les réseaux de communication, les routes d'aviation, les réseaux électriques, etc. où les poids peuvent être des tarifs, des distances, des résistances, ... . Un réseau peut être un modèle de relations entre les élèves - une arête représentant une amitié entre deux personnes. Parfois on peut utiliser des arêtes dirigées (avec des flèches) pour représenter des rues à sens unique, par exemple. Bien que ces applications soient intéressantes, on peut faire l'étude de réseaux simplement parce que l'on aime ça. A cette fin, il existe un grand nombre de livres et manuels sur le sujet de la théorie des graphiques (voir [5] par exemple). Malheureusement ces ressources sont pour le niveau secondaire et doivent être adaptées pour les classes de maternelle à la 8e année. En gardant les exemples assez simples, il est possible d'utiliser ces idées dans les classes élémentaires et intermédiaires.

Figure 4

Nous terminons avec d'autres suggestions.

i) Revenons au problème de la section 2. Le conducteur du chasse-neige sait qu'il doit nettoyer les routes en faisant un arbre, mais puisqu'il est payé à l'heure, il préfère porter au maximum le temps total pour nettoyer les routes. Comment va-t-il choisir les routes maintenant?

ii) Ignorons le problème de la section 2, mais utilisons la carte dans la figure 3 où les poids représentent maintenant les distances entre les maisons. Choisissons une des maisons pour la nôtre. Comment trouver la distance la plus courte pour aller de notre maison à toutes les autres maisons? La solution varie dépendant de quelle maison nous avons choisie pour la nôtre. Ce problème est un peu plus difficile, mais avec un exemple aussi petit, c'est un problème raisonnable et devrait engendrer de bonnes discussions en classe.

Figure 5

Les problèmes mentionnés dans cet article sont présentés dans l'unité modèle pour la 5e année du programme d'études Mathématiques, Programme d'études pour l'élémentaire [3]. Evidemment la taille et la difficulté du problème peuvent être adaptées pour presque tous les niveaux. Par exemple, on peut changer les problèmes en utilisant la route que suit la livreuse de journaux quand elle délivre les journaux des deux côtés de la rue à la fois, ou la route que prennent les éboueurs avec leur camion (le problème est différent si les déchets sont ramassés des deux côtés de la rue à la fois ou si ils sont ramassés un côté de la rue à la fois). Ces problèmes permettent aux élèves de tester et vérifier leurs hypothèses, ainsi que discuter leurs idées en groupes coopératifs. Une évaluation du travail des élèves peut se faire à l'aide de fiches anecdotiques, de rapports écrits ou de grilles d'observation.

References

1. Curriculum and Evaluation Standards for School Mathematics, N.C.T.M., 1989.

2. Everybody Counts, A Report to the Nation on the Future of Mathematics Education, National Research Council, Washington D.C., 1989.

3. Mathématiques, Programme d'études pour l'élémentaire , ministère de l'Education, 1993.

4. Mathematics, Charting the Course, Summary and Recommendations, Saskatchewan Education, (1989).

5. Robin J. Wilson, Introduction to Graph Theory, 3rd. edition, Longman Group Ltd., 1985.