Our solution combines parts of the solutions sent in by Normand Laliberté (Kitchener, Ontario) and by Juan Mir Pieras (Spain). Their entire solutions may be read on our French and Spanish pages (respectively). Alexdander Potapenko (Russia) has sent us a solution that is quite similar to our featured solution. He added the comment that since the argument does not involve the notion of dimension, the result also holds for points in 3 or more dimensions. We must first agree on what an n-gon is.
Definitions. An n-gon in the plane is a sequence P0, P1,..., Pn-1 of n (not necessarily distinct) points. The points are called vertices and the segments joining consecutive vertices P0P1, P1P2, ...Pn-1P0, are called sides. In particular, a pentagon is the ordered 5-tuple P0P1P2P3P4, and its sides are P0P1, P1P2, P2P3, P3P4, and P4P0.
Note that our definition allows any number of the vertices of an n-gon to be collinear or to be repeated, and the sides may cross one another. Although an arbitrary set of n points in the plane determines as many as n!/(2n) different n-gons, an ordered set of n points determines a unique n-gon. For our problem we need not worry about the n-gon's shape, although we will look at that issue later.
Solution to part a.
You are given five points in the plane and are told that they are the midpoints of the edges of some pentagon. Find the pentagon.
We denote the midpoint of the segment PiPi+1 by Mi; to simplify matters we shall use capital letters to stand both for a point and for the vector from some fixed origin to that point. Thus, Mi satisfies the equation
We are given the five midpoint vectors M0, M1, M2, M3, M4, and are asked to find the unknown vertex vectors P0, P1, P2, P3, P4. We therefore have 5 equations in the 5 unknowns,
.
.
.
P4 + P0 = 2M4.
These can be solved successively to get
P0
= 2M0 - P1
= 2M0 - 2M1 + P2
= 2M0 - 2M1 + 2M2 - P3
.
.
.
= 2M0 - 2M1 + 2M2 - 2M3 + 2M4 - P0.
Thus, for any five given points Mi, the initial vertex P0 is determined uniquely as the tip of the vector
and similarly for the other four vertices.
Solution to part b.
Given the midpoints of the sides of an n-gon in the plane, is it always possible to determine the n-gon?
For n odd the answer is yes, there is always a unique n-gon P0P1ÉPnÐ1 whose midpoint figure is the given n-gon M0M1...Mn-1. Specifically, the argument given for n = 5 can be extended to show that the initial vertex P0 satisfies
Remark. For n = 3 the result is a familiar Euclidean theorem: Since P0 = M0 - M1 + M2 implies P0 - M0 = M2 - M1 we see that the midpoint triangle M0M1M2 has its sides parallel to the sides of the initial triangle P0P1P22 and half as long. When M0M1M2 is a nondegenerate triangle, one can construct P0P1P2 as the triangle whose sides lie on the lines through the vertices of M0M1M2 that are parallel to the opposite side.
For n even the answer is no, it is not always possible to determine the n-gon; moreover, when a solution exists, then there are infinitely many polygons whose midpoint figure is the given set of points. When n is even our argument above leads to the equation
which is consistent if and only if
To find the vertices we can take any point to be P0 and define P1 = 2M0 -P0. We proceed recursively by defining Pi+1 = 2Mi -Pi for i up to n-1. Then Pn = P0 (so that the n-gon is well defined) if and only if (*) holds.
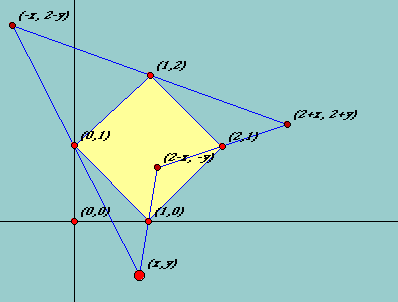
Remark. For n = 4 we again have a familiar result: this is the converse of the theorem that tells us that the midpoint figure of any quadrangle is a parallelogram. Here (*) is the condition that M0 - M1 + M2 - M3 =0. This says that M0M1M2M3 is a parallelogram, so that it qualifies as the midpoint figure of an infinite family of quadrangles - one for each choice of P0. In the example below, suggested by Laliberté, the midpoint figure is a square and the point P0 is (x, y). Note what happens as P0 is moved about the plane, for what positions the quadrangle becomes convex and where it degenerates into a triangle.
Further comments.
In his solution Mir brought up the question of when P0P1...Pn-1 might be convex. He defines an n-gon to be convex if it satisfies the two conditions (i) sides can intersect only at a vertex, and (ii) all vertex angles are less that a straight angle. It is easily seen that for P0P1...Pn-1 to be convex the midpoint figure M0M1...Mn-1 would necessarily be convex. But it is also easily seen that the convexity of the midpoint figure does not force the original polygon to be convex: start with a convex n-gon P0P1...Pn-1 with a "large enough" angle at P0, then reflect P0 in the line Pn-1P1 to get a nonconvex
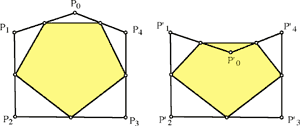
n-gon P'0P1...Pn-1 whose midpoint figure is convex. There seems to be no simple condition on an arbitrary midpoint figure to insure the convexity of P0P1..Pn-1. On the other hand, there is an interesting theorem that gets rediscovered from time to time which says that midpoint figures are generally "more convex" than the original polygon. Starting with an n-gon whose vertices are in general position, define a sequence of n-gons by successively taking midpoint figures Ñ that is, the kth polygon is the midpoint figure of the (kÐ1)st. The polygons in the sequence become affinely regular in the sense that for k large enough, there is a linear transformation that takes the kth midpoint figure of the sequence arbitrarily close to a (convex) regular n-gon. See "A Periodicity Problem in Plane Geometry" by Daniel B. Shapiro [American Mathematical Monthly 91:2 (Feb. 1984), pages 97-108] for the precise statement and numerous references.