To mark the arrival of spring, our monthly problem pays tribute to Canadian cuisine.
- In a large bowl, mix together one egg, one cup of milk, one cup of flour, a teaspoon of baking powder, and a pinch of salt. You get something called pancake batter.
- Drop one big spoonful of the batter into a hot greased pan and cook on both sides for approximately 17 minutes. You get something called a burnt pancake.
- Put the burnt pancake on a sheet of paper and trace its contour with a pencil. You get something called a simple closed curve.
- Prove that your simple closed curve contains the three vertices of an equilateral triangle.

We received correct solutions from John Campbell (Edmonton), Juan Mir Pieras (Spain), Alexander Potapenko (Russia) and Gordon Robinson (Victoria). Each of the respondents observed that solving the problem for the boundary of a pancake is much easier than solving the problem for the boundary of an arbitrary region in the plane. We shall discuss the general case after looking at our three submitted solutions. Each construction is valid as long as the initial vertex is taken to be any point where the boundary is "sufficiently smooth."
I. Solution by Alexander Potapenko and Gordon Robinson.
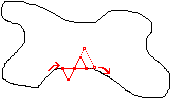
Fix any point A on a smooth part of the boundary, and choose a second point B on the boundary sufficiently close to A so that the equilateral triangle ABC has its third vertex C in the interior. With A fixed, move B along the curve while moving C so that the triangle ABC remains equilateral (as in the figure). The vertex C will move in a complicated way, but when B approaches A from the other side, C will be outside the bounded region. Thus, there must have been at least one position of the moving triangle where C crossed our curve, and at this moment all vertices of our equilateral triangle are on the curve.
II. Solution by John Campbell and Gordon Robinson.
Let S be a simple closed curve and let A be a point on S such that the tangent at A is defined. Using A as the centre of rotation, rotate S about A through 60 degrees to get the new curve S' through A. Locally, the picture looks like
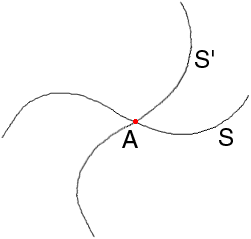
Since a portion of S' is inside the region bounded by S and a portion of S' is outside, because S is continuous and closed there must be a point, call it C, where the two curves intersect for a second time. If B is the point of S that was rotated to C, then both B and C are points of S that are equidistant from A; moreover angle BAC = 60o. Thus, A, B, C all lie on S and are the vertices of an equilateral triangle.
III. Solution by Juan Mir Pieras.
Let A be a point on a smooth part of the boundary, and let D be a point of the boundary whose distance from A in the plane is as large as possible. Orient the pancake so that A is at the bottom and D is somewhere above. Take a point R of the boundary near A on the right, and a point L on the boundary to the left so that AL = AR. Now move R counterclockwise around the curve and L clockwise in such a way that the distance AL always remains equal to the distance AR. At the start the angle RAL was approximately equal to 180o, while at the final point D the angle will be 0o. Somewhere along the way there will have to be at least one position where angle RAL = 60o. At that moment R, A, L will be points of the boundary at the vertices of an equilateral triangle.
Comments on simple closed curves.
We have been assuming that the boundary of our pancake is a curve that can be easily drawn - it is smooth with only a small number of wiggles (inflection points). To a topologist a simple closed curve can be very unsimple - so much so that they prefer to call them Jordan curves. Specifically, a Jordan curve is described by the set of points (x(t), y(t)) where x(t) and y(t) are continuous real-valued functions on the unit interval (with t running from 0 to 1) such that
(ii) for 0 <= s < t < 1,
the point (x(s), y(s)) is different from the point (x(t), y(t)).
The Jordan curve theorem (published by Camille Jordan in 1893) says that such a curve separates the plane into two regions, the interior (which is bounded by the curve) and the exterior (which is unbounded). Of course, if one imagines the Jordan curve to be the boundary of a pancake, such a result is obvious - the interior is the part you eat. However, the boundary of a Jordan curve might oscillate wildly back and forth (like sin (1/x) near x = 0), or even look like a fractal. In these extreme cases there is no practical way to determine whether a point belongs to the interior or the exterior! The classic topology book by Edwin Spanier devotes much of its first 200 pages to proving the theorem (in its n-dimensional version).
Even the most complicated Jordan curve admits an inscribed equilateral triangle. In fact, solution (I) easily can be modified to produce equilateral triangles for infinitely many positions of the point A. A careful argument can be found in [Victor Klee and Stan Wagon, Old and New Unsolved Problems in Plane Geometry and Number Theory. Mathematical Association of America (Dolciani Math. Expositions, No. 11), 1991], Theorem 11.3, pages 61-62. They begin with a small circle in the interior of the Jordan curve - this is always possible by the Jordan curve theorem. They then slide the circle to where it touches the curve (so that the interior of the circle is still inside the curve). Call A any point where the circle touches the curve, and let B and C be points inside the circle so that ABC is an equilateral triangle. Next, move B and C away from A along the sides of the angle at A (keeping A and the rays AB and AC fixed), until one of them, say B, meets the curve. The proof concludes just as in solution I above.
To see what can go wrong when we try to apply solution II to an arbitrary Jordan curve, take for the boundary S a triangle PQR with an angle at P less than 60 degrees. If the fixed point A is taken to coincide with P, then the rotated image S' will not intersect S a second time. Of course, if you choose A to be any point on the sides of PQR, then Campbell's solution II goes through without any difficulty.
As for solution III, we are not yet sure what conditions must be imposed on our Jordan curve to make the argument work. Possibly all we need is for the curve to be smooth (with the derivatives of x(t) and y(t) both continuous). The difficulty is that the boundary can rrepeatedly come close to the fixed point A. Remember that we require R and L to move around the curve while keeping their distances from A equal; consequently, it is conceivable that the moving points R and L will never succeed in arriving at the position where angle RAL is 60 degrees because they will forever be forced to retrace their path.