A problem from Denmark's "Georg Mohr Konkurrencen I Matematik 1996" was generalized by Pierre Bornsztein [CRUX MATHEMATICORUM 2001, page 240]. He showed that if (a) P is a permutation of the set {1, 2, ..., n}, and (b) n is congruent to 2 or 3 modulo 4, then the numbers |k - P(k)| cannot be distinct. Our problem for August is to say what happens when n = 20:
We received correct solutions this month from Juan Mir Pieras (of Spain) and Gordon Robinson (of Victoria, British Columbia). Not only did Mir answer the question for n = 20, but he constructed the appropriate permutation for all n congruent to 0 and 1 modulo 4. Robinson included with his answer a proof of Bornsztein's result that there can be no such permutation when n is congruent to 2 or 3 modulo 4.
Mir's Solution.We construct permutations
p(k) on the set {1, 2,..., n} for which D(k) = |k - p(k)| takes on all values from 0 to n - 1 when n of the form 4m and 4m + 1.For n = 4m define p(k) by
| p(k) equals | for | D(k) takes on the following values |
|---|---|---|
| 4m + 1 - k | 1 <= k <= m | odd numbers from 2m + 1 to 4m - 1 |
| m + 1 | k = m + 1 | 0 |
| 4m + 2 - k | m+1 < k <= 2m | even numbers from 2 to 2m - 2 |
| 4m + 1 - k | 2m < k < 3m | odd numbers from 1 to 2m - 3 |
| 4m - k | 3m <= k | even numbers from 2m to 4m - 2 |
| 2m + 1 | k = 4m | 2m - 1 |
In particular, for m = 5 -- that is, for n = 20 -- the permutation looks like
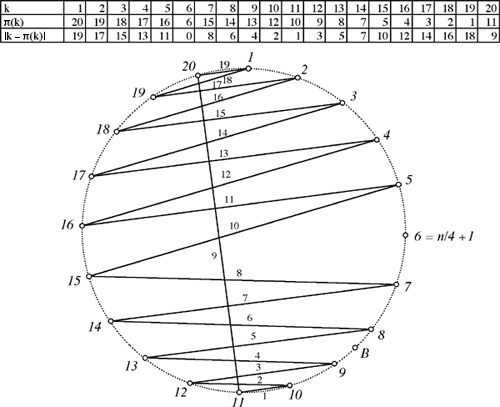
The case n = 4m + 1 is quite similar:
| p(k) equals | for | D(k) takes on the following values |
|---|---|---|
| 4m + 2 - k | 1 <= k <= m | even numbers from 2m + 2 to 4m |
| m + 1 | k = m + 1 | 0 |
| 4m + 3 - k | m+1 < k <= 2m + 1 | odd numbers from 1 to 2m - 1 |
| 4m + 2 - k | 2m + 1 < k <= 3m | even numbers from 2 to 2m - 2 |
| 4m + 1 - k | 3m < k <= 4m | odd numbers from 2m + 1 to 4m - 1 |
| 2m + 1 | k = 4m + 1 | 2m |
Here is an example with n=9 (that is, with m = 2):
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| p(k) | 9 | 8 | 3 | 7 | 6 | 4 | 2 | 1 | 5 |
| D(k) = |k - p(k)| | 8 | 6 | 0 | 3 | 1 | 2 | 5 | 7 | 4 |
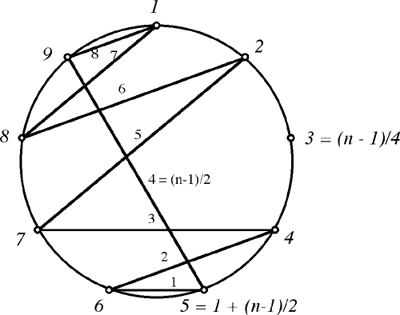
This ends the general solution. Mir continues by pointing out that these are not the only permutations that solve the problem. First, there are two obvious symmetries. A permutation p(k) can be represented by an n by n chessboard with a marker in the kth row and p(k)th column Ñ these markers represent a permutation of the set {1, ..., n} when there is exactly one marker in each row and in each column (like n nonthreatening rooks on an n by n chessboard). Our permutations satisfy the additional requirement that no two markers can have the same distance from the diagonal k = p(k). It is evident that these conditions are preserved by reflection in either diagonal of the chessboard; more precisely, if the permutation p(k) satisfies the conditions of the problem then so do
p-1(k), and
n + 1- p-1(n + 1 - k).
Note that none of these four permutations can be equal, hence, for n = 4m or n = 4m+1 the number of permutations satisfying the conditions of the problem is a multiple of 4. The number of these permutations grows rapidly with m, as follows. [We take Mir's word for the following numbers.]
| n | number of distinct permutations | n | number of distinct permutations |
|---|---|---|---|
| 4 | 4 x 1 | 5 | 4 x 1 |
| 8 | 4 x 8 | 9 | 4 x 24 |
| 12 | 4 x 248 | 13 | 4 x 628 |
| 16 | 4 x 12628 | 17 | 4 x 36036 |
Finally this month, for the convenience of readers with no access to Crux Mathematicorum with Mathematical Mayhem we shall reproduce Pierre Bornsztein's neat argument from May, 2001 (Volume 27:4) page 240 that no such permutation exists when n is congruent to 2 or 3 modulo 4. More precisely, he assumes that p is a permutation of {1, ..., n} and |p(k) - k| is a permutation of {0, ..., n - 1}, and then shows that n must be congruent to 0 or 1 modulo 4. Our conditions on p imply that S(p(k) - k) = 0 and
Moreover, since |j| - j must be even for all integers j, for some integer d we have
Comparing (1) and (2), we get n(nÐ1) = 4d, which implies that n is congruent to 0 or 1 modulo 4 as claimed.
Gordon Robinson provided a similar argument; here is how he explains the conclusion:
Crux with Mayhem, a journal published by the Canadian Mathematical Society, is a rich source of interesting problems. For more information, see http://journals.cms.math.ca/CRUX/.