January 2002 solution

Solution to January 2002 Problem

For each real number r, let T_r be the transformation of the plane that takes the point (x, y) into the point (10^r x, y + r). Find the equation of the continuous curve y = f(x) that contains the image of the point (2002, 2002) for every transformation T_r.

Solution.

We received correct solutions from (in alphabetical order) Normand Laliberté (Ontario), Juan Mir Pieras (Spain), Alexander Potapenko (Russia), Eulogio Ruiz González (Spain), and Alex Wright (the internet). Since all solutions were substantially the same, we will present a combination of them. The main difference among the approaches was in notation: here we shall let log x stand for the base-10 logarithm. This means that log (10^r) = r.

We are told that T_r takes (2002, 2002) to (10^r(2002), 2002 + r). That is, for any r

x = 10^r(2002)

y = 2002 + r Taking the logarithm of both sides of the first equation we get log x = r + log 2002. To eliminate the parameter r, plug r = log x - log 2002 into the equation for y to get y = f(x) = log x + 2002 - log 2002. If you prefer, since log 2002

3.3, f(x)

log x + 1998.7.

Alternatively, in terms of the natural logarithm the answer becomes

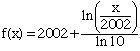
Comment. This month's problem illustrates an important property of the logarithm function. When the parameter r is taken to be 1, our transformation T takes the point (x, y) to (10x, y + 1), and it takes that point to (102x, y + 2), and that point to (103x, y + 3), and so on. As the x coordinate increases geometrically, the y coordinate increases arithmetically. As our problem illustrates, this action slides the point along the logarithm curve y = log x + c (for some constant c).