Introduction.
For July we look at the problem of fitting an equilateral triangle
inside a triangle T labeled with sides a >= b >= c. Note that the angles
opposite these sides are ordered A >= B >= C. It is not hard to show that
when the middle angle B is at most 60 degrees, the largest equilateral
triangle that fits in T rests on the longest side a. When B >= 60 there is
a condition involving a, c, and B that tells whether the largest
equilateral triangle in T will rest on the longest side a or on the
shortest side c. That formula can be found in "Equilateral Triangles in
Triangles," a paper by Richard P. Jerrard and John E. Wetzel that will
appear in the American Mathematical Monthly later this year.
The Problem For July.
Describe the unique nonequilateral triangle for which the three largest
inscribed equilateral triangles, one on each side, are equal.
Juan Mir Pieras (of Spain) Boting Yang (of Regina) and Gordon Robinson (Victoria) sent in correct solutions this month, but Mir single-handedly made up for the summer slack by submitting three! One is based on trigonometry, one is more geometric, and the third is based on similar triangles. We use on this page his geometric solution combined with Yang's; the other two solutions can be found on our Spanish page.
Solution.
Let T be the triangle ABC. We use the convention that in T, sides a = BC, b = CA, and c = AB. Furthermore, the sides are labeled so that a >= b >= c.
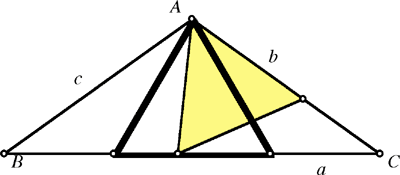
We first show that b = a (that is, the triangle is isosceles with AC = BC). The introductory comments tell us (and it is easy to show) that the largest equilateral triangle that fits in T sits on either side a or side c; the only way an equilateral triangle on the middle side b could be largest would be when b = a or b = c. However, we can quickly eliminate the possibility that the two shortest sides are equal:
An Isosceles triangle ABC whose shortest sides are equal
If sides b and c were equal and shorter than a, the largest equilateral triangle on side a would necessarily be larger than any equilateral triangle on b (as in the figure). Since the given triangle T is not equilateral, the only possibility that remains is for the two largest sides to be equal; that is, a = b.
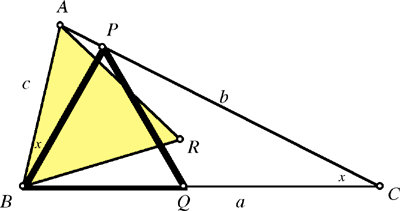
An isosceles triangle ABC whose longest sides are equal
Because T is isosceles with a = b the longest sides, the angles at A and at B are equal and greater than 60o. Consequently, the largest equilateral triangle on side a necessarily shares an angle with B; call it triangle BQP as in the figure. Also, the largest equilateral triangle on side c has one side equal to AB; call that triangle ABR. We are given that these two equilateral triangles are equal, which implies that BA = BP, so the triangle BPA is isosceles. Since the isosceles triangles ABC and PAB share the angle BAC, the triangles ABC and PAB are similar. In particular, angle ACB = angle PBA = x. From angle BAC = angle CBA = 60o + x we deduce that the angles of T satisfy (60o + x) + (60o + x) + x = 180o; thus, x = 20o. We conclude that T has angles 20o, 80o, and 80o as claimed.