Solution to June 2002 Problem

The Seven Dwarfs are having breakfast, and Snow White has just poured them some milk. Before drinking, the dwarfs have a ritual. First, Dwarf #1 splits his milk equally among his brothers' mugs (leaving himself with nothing). Then Dwarf #2 does the same with his milk, etc. The process continues around the table, until Dwarf #7 has distributed his milk in this way. (Note that Dwarf #7 is named Dopey!) At the end, each dwarf has exactly the same amount of milk as he started with! If the total amount of milk was 42 ounces, how much milk did each dwarf have at the beginning? Is this the only possible distribution of milk, or does the problem admit multiple solutions?

The source of this month's problem is the US-Canada Mathcamp 2002 Application Quiz.

We received solutions from six of Snow White's friends, namely John Campbell (Edmonton, Alberta), Normand Laliberté (Kitchener, Ontario), Juan Mir Pieras (Spain), Penny Nom (Regina), Alexander Potapenko (Russia), and Gordon Robinson (Victoria, British Columbia); they all deserve an entire glass of milk. Everybody agrees that the distribution of milk among the seven dwarfs (in ounces) is

12, 10, 8, 6, 4, 2, and 0. You should check that this distribution is correct by noting that the "arithmetic" sequence has the property that when dwarf 1 gives two ounces of his milk to each of his comrades, the effect is the same as if each dwarf passed his cup to the next. In other words, the numbers in the distribution do not change. Robinson, Mir, and Potapenko all generalized the problem to n dwarfs and M units of milk. The initial distribution would then be k(n-1), k(n-2), k(n-3), ..., k, 0, where k = M/(1 + 2 + ... + n-1). For notational simplicity, let us stay with the original problem where n = 7 and M = 42.

The rules immediately imply that the seventh dwarf starts and ends with an empty mug: the ritual ends when dwarf 7 has emptied his mug, at which time he has exactly the same amount of milk as he started with. The problem is to show that there can be no distribution other than the arithmetic sequence that descends to zero. The explanations that we received fall roughly into three categories. We shall present one in detail, then outline the other two.

Solution 1 (Potapenko and Robinson).

Potapenko and Robinson had very similar approaches, but they started at different ends. Combining their work leads to a very simple argument. For i = 1, 2, ..., 7, let

si denote the amount of milk dwarf i started (and ended) with, and

ri denote the total amount of milk dwarf i received before he distributed his milk to the others.

The rules of the ritual lead to two simple equations:

. This says that the total received by dwarf i+1 equals the amount the previous dwarf received in the first iÐ1 rounds plus the amount he gets from that dwarf. For example, r3 (the amount received by dwarf 3) equals the amount that comes from dwarf 1 (namely r2 = s1/6) plus the amount he gets from dwarf 2 (namely  (s2+r2)/6).

Note that si (the amount dwarf i begins with) equals the amount received from all dwarfs whose turn came after his. So, for example, dwarf 2 received the same amounts as dwarf 3 (namely s3) plus the amount dwarf three gave him (namely  (s3+r3)/6).

These two systems of equations (12 equations in all) allow us to determine the relative values of the si. We start with ri = 0 and any specified amount of milk in the first glass. (We take s1=12 to make the total come out to 42 ounces.) We then compute r2 using equation 1 (getting r2 = 0 + (12+0)/6 = 2), which allows us to compute s2 using equation 2 (namely 7s2 = 6s1 - r2, so that s2 = 70/7 = 10). We continue to alternate the use of equations 1 and 2 until we have found all si and thereby proved that the initial distribution we described above is the only possible solution.

Solution 2 (Campbell and Mir).

The instructions lead naturally to seven equations in the seven unknowns si (where, as in the previous solution, si is amount of milk dwarf i started (and ended) with). In vector notation, we seek the column vector s = (s1, s2, ..., s6, s7). The first stage of the ritual corresponds to taking s to As, where A is the 7 by 7 matrix

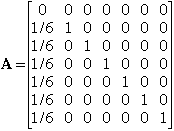
The next stage is represented by a matrix B which is obtained fromA by interchanging the first two rows and then the first two columns Ñ its first column is 1 followed by 6 0s, while its second column is 1/6, 0, 1/6, ..., 1/6. Continuing in this way we get matrix C from A by interchanging rows 1 and 3 then columns 1 and 3, and so on up to matrix G (interchanging rows 1 and 7 and then columns 1 and 7). Let us denote the product of these matrices by P = GFEDCBA. In matrix notation our problem is to solve

(3)      Ps = s and show that when s1 + ... + s = 42, the solution is unique. Since we already know a solution, the problem reduces to showing that the solution space in equation (3) is one-dimensional. We see no easy, direct way to accomplish this, so we abandon this method and turn to an indirect argument. (For those who know the Perron-Frobenius theorem, the matrix argument is easily completed; that theorem, however, is generally considered an advanced topic in linear algebra.)

First, we pass along a suggestion from Gordon Robinson. Readers with access to a spreadsheet might want to try the following computer experiment that illustrates the power of the Perron-Frobenius theorem. Carry out the pouring process not for just one complete cycle of the ritual, but repeatedly for a number of complete cycles. It will be seen that whatever the distribution of the original 42 ounces, the final distribution quickly converges to the 12, 10, 8, 6, 4, 2, 0 sequence! That amounts to applying the matrix P repeatedly to an arbitrary vector of length 7 whose entries (positive or negative) sum to 42.

Solution 3 (Penny Nom).

For this approach we need the basic fact (from the second solution) that if both s =(s1, s2, ..., s6, 0) and s' = (s'1, s'1, ..., s'6, 0) satisfy the pouring conditions of the problem and we temporarily allow amounts of milk different from the specified amount M = 42, then s + s' and ks also satisfy the pouring conditions for any real number k. (This claim simply states that the solution space to (3) forms a vector space.) Next we suppose, to the contrary, that there is a solution s' different from our known solution (12, 10, 8, 6, 4, 2, 0). We choose the smallest possible positive number k so that s - ks' = (s1-ks'1, s2-ks'2, ..., s6-ks'6, 0) has all si-ks'i to be zero and the rest to be nonnegative. We now pour si-ks'i ounces of oil into the ith cup for each i. This oil has the property that it floats above the milk that is in the cup. We go through the pouring ritual with the oil and milk mix, stirring the mixture so that each dwarf gets his share, namely 1/6 of the milk from the glass being emptied and 1/6 of the oil. At the end, each dwarf has the same amount of milk and the same amount of oil that he started with --- that's because s and s - ks' are both solutions. However, s - ks' is a solution that has two dwarfs --- dwarf i and dwarf 7 --- starting with no oil. Because dwarf number i receives oil from all the dwarfs that follow him, this situation implies that dwarf 7 had nothing to give, which in turn implies that sj-ks'j = 0 for all j. This contradicts our assumption that there is a solution s' different from our known solution, so that our known solution is necessarily unique.