Your enemy gets to choose 2000 of the counting numbers from 1 to 3000. Your job is to find a subsequence of 1000 of your enemy's numbers so that they alternate odd, even, odd, even, ... when listed in their natural order. Prove that no matter how clever your enemy might be, you can always succeed.

We thank Aart Blokhuis of Eindhoven University of Technology for March's problem. He devised it for the past year's Dutch Mathematical Olympiad. Five correct solutions were submitted this month:

Two of these were clever and quite similar, but the others were each clever and quite different from one another. It is interesting to look at all four solutions and see what they have in common.

Solution 1. Submitted independently by Francesco Barioli and Juan Mir Pieras.

Consider the 1500 pairs of numbers (1, 2), (3, 4), (5, 6), ..., (2999, 3000). In choosing 2000 numbers, our enemy has eliminated the other 1000 numbers. That means that at most 1000 of the pairs could contain one (or two) of those missing numbers. We are therefore left with at least 500 complete pairs - that is, number pairs whose entries were both chosen by the enemy. We simply take five hundred of those complete pairs for our sequence of 1000 numbers ordered odd, even, odd, even, ... .

Solution 2. Submitted by Gordon Turpin.

Consider the sequence of numbers chosen by the adversary in their natural order. The entire sequence would exhibit odd-even alternation if it were not for intervening sequences of missing numbers (numbers not chosen). Of these contiguous sequences of missing numbers, we note that

only odd-length sequences can interrupt the odd-even alteration of chosen numbers.

We choose our subsequence of the adversary's sequence as follows: remove the chosen number immediately following each odd-length sequence of missing numbers. This turns all odd-length missing number sequences into even-length missing number sequences and costs us one chosen number per odd-length to even-length conversion. The shortest odd-length missing number sequence is of length 1. There are 1000 missing numbers in all, so at most 1000 odd-length sequences. Changing all odd-length missing sequences to even-length will thus cause the removal of at most 1000 numbers from the sequence of 2000 chosen by the adversary.

We are left with at least 1000 number in odd-even alternation.

Solution 3. Submitted by Alexander Potapenko.

We again look at the holes in the sequence chosen by the enemy, but in a different way: The sequence is x₁, x₂, ..., x₂₀₀₀, and we put
y₁ = x₁ - 0, y₂ = x₂ - x₁, y₃ = x₃ - x₂, ..., y₂₀₀₀ = x₂₀₀₀ - x₁₉₉₉. Then for each n we have

For this purpose, we define Y_odd to be the average of all odd numbers in the y-sequence, and Y_even to be the average of all even numbers in the y-sequence. Of course, if the y-sequence does not contain any even numbers, then Y_even does not exist, but then a = 2000 and we are done.

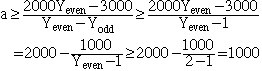
Solution 4. Submitted by Penny Nom.

Penny gave us a variation of Alexander's argument, showing that in fact, at least 999 of the differences y₂, y₃, ..., y₂₀₀₀ are equal to 1:
We have

The rest of her argument goes as follows: Consider a longest subsequence a₁, a₂, ..., a_p alternating between odd and even numbers. Then the terms x_i that come before a₁ must all have the same parity as a₁, so that x_i+1 - x_i is at least 2. Similarly, the terms x_i that come after a_p all have the same parity as a_p, so that x_i - x_i-1 is at least 2. From a_j to a_j+1, the terms x_i can switch parity only once (otherwise it would be possible to enlarge our subsequence), so there is at most one term x_i - x_i-1 equal to 1. Therefore, p - 1 is at least 999, so p is at least 1000.