The theatre charges one dollar for its Sunday afternoon show. One Sunday the cashier finds that he has no change. Eight people arrive at the theatre; four have only a one-dollar coin (a loonie) and four have only a two-dollar coin (a toonie). Depending on how the people line up, the cashier may or may not be able to make change for every person in the line as they buy their tickets one at a time. Suppose that the eight people form a line in random order, without knowing who has a loonie and who has a toonie. What is the probability that the cashier will be able to make change for every person in the line?

This month's problem is taken from the 2001 British Columbia Colleges High School Mathematics Contest.

We can interpret the problem as producing a random sequence consisting of four Ls (loonies) and four Ts (toonies). In the solution of Potapenko, which we present later, he pictures this sequence as a polygonal path that starts at the origin (0, 0) and moves to the right by going one step up with slope 1 when there is an L, and one step down with slope —1 when there is a T. For example,

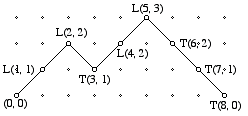
represents the sequence LLTLLTTT. Any path that corresponds to four Ls and four Ts must likewise start at the origin and end at (8, 0). The number of these sequences equals the number of ways to choose the position for the four Ls from among the eight terms in the sequence. Thus

the number of polygonal paths =
.

The situation of interest in our problem is when the number of Ls that have appeared in the sequence is never less than the number of Ts; this is represented by a path that never goes below the x-axis. We shall call such a path good. George Pólya in section 3.5 of his book, Mathematical Discovery (Wiley, 1981) popularized a neat method for counting good paths. It is based on the simple observation that since each vertex along a path comes from either an L (going up) or a T (coming down), it has at most two predecessors. If there are s paths to one of the predecessors and t to the other, then there must be s + t paths to our vertex. Applying this rule with the origin as initial point we get the following diagram, in which the label at each vertex indicates the number of paths to that point that never cross the x-axis.

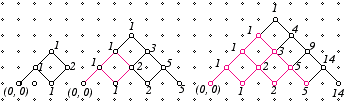
We therefore have 14 good paths (paths that never cross the x-axis). This number together with the previous count says that the probability that a random sequence of four Ls and four Ts corresponds to a good path is 14/70 = 1/5, which is the solution to our problem of the month.

Alternative Solution by Alexander Potapenko, (Russia).

It is just as easy to deal with the more general question in which there are n toonies and n loonies. Restating the problem as providing a random sequence of n Ls and n Ts, we want to know the probability that the Ls are arranged so that the corresponding polygonal path is good. More precisely, we have a path that starts at (0, 0), goes up to the right when there is an L in the given sequence, and down to the right when there is a T. Because there is an equal number of Ls and Ts, the path must end at the point (2n, 0). It is called good if it starts with an L and never crosses the x-axis, and bad otherwise. We shall see that the probability that a random path is good is 1/(n+1).

The number of all possible paths is

.

Instead of counting the number of good paths, we shall instead count the number of bad paths. The reason for this is that

This last number is easily calculated.

To prove the claim, suppose that P is a bad path. That means that it has at least one vertex below the x-axis. We transform that bad path by reflecting the portion of the path to the right of the first bad point in the horizontal line y = —1 (which passes through that point). Here is an example that represents the sequence LTTLLTTTLL. Note that

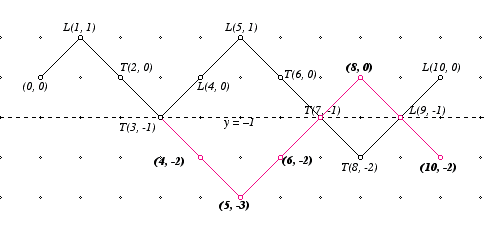
the reflection interchanges the vertex (x, y) of the given path with the point (x, —2—y) on the pink path. In other words, to any given bad sequence of n Ls and nTs there corresponds a path that starts at (0, 0) and ends at (2n, —2); conversely, to any path that starts at (0, 0) and ends at (2n, —2) there corresponds a bad sequence. Of course, the paths that start at (0, 0) and end at (2n, —2) correspond to a sequence of n — 1 Ls and n + 1 Ts. Their number is therefore

.

Consequently, the probability of of a random path being bad is

.

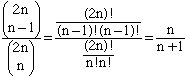Finally, we see that the probability of a random path being good is

.

Comment. Potapenko's solution shows that the number of good paths is

.

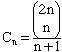The numbers C_n are called the Catalan numbers. These remarkable numbers arise in a great variety of contexts; for example, C_n is the number of ways of associating a product of n + 1 terms. Among the dozens of ways of deriving the formula, one particularly elementary approach is given by David Singmaster in his article, "An Elementary Evaluation of the Catalan Numbers" in The American Mathematical Monthly 85:5 (May, 1978), pages 366-368. The bibliography there provides a glimpse at the vast literature dealing with Catalan numbers.

We received other nice solutions from Normand Laliberté (Ontario) and from Juan Mir Pieras (of Spain). They both developed recursive formulas that lead to a solution quite similar to the first solution given above. You can find their arguments on our French and Spanish web pages, respectively.